Е1 =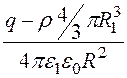 +
+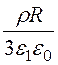 ; j 1 = -
; j 1 = -![]() =
=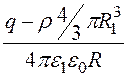 –
–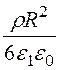 + А1.
+ А1.
В области R2 < R < R3
Е2 =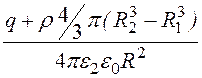 ; j 2 = -
; j 2 = -![]() =
=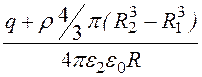 + А2.
+ А2.
Пусть j 2(R4) = 0, тогда
А2 = -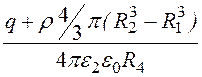 ; j 2(R) =
; j 2(R) =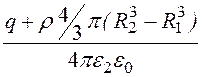
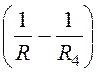 .
.
Потенциал металлической прослойки j1(R2) = j2(R3). Отсюда
А1 =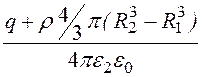
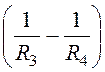 –
–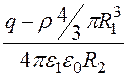 +
+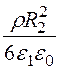 ;
;
j1(R) =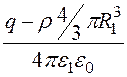
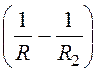 +
+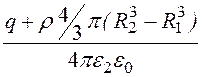
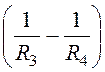 –
–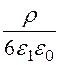 (R2 – R22).
(R2 – R22).
Напряжение, приложенное к устройству,
U = j 1(R1) =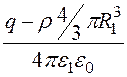
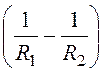 +
+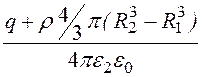
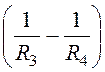 –
–
–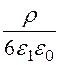 (R12 – R22) = q·
(R12 – R22) = q·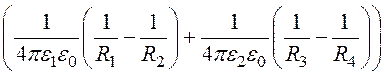 –
–
–
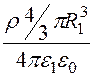
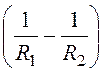 –
–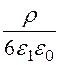 (R12 – R22) +
(R12 – R22) +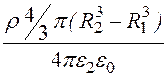
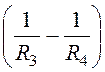 =
=
= 3,447·1011·q + 1117.
Отсюда q =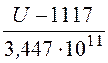 =
-3,406·10-10 Кл.
=
-3,406·10-10 Кл.
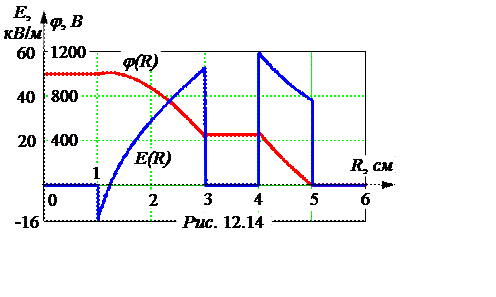
С учетом значения заряда q получаем окончательные формулы потенциала и напряженности поля, на основании которых строим требуемые графики (рис. 12.14):
j(R) =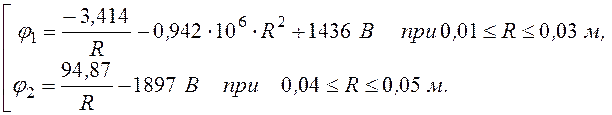
Е(R) =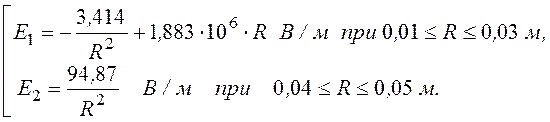
 Примечание. C
помощью ПЭВМ в системе MathCAD задача может быть решена без столь громоздких
выкладок, а путём составления и решения системы уравнений, как это показано в
задаче 12.46.
Примечание. C
помощью ПЭВМ в системе MathCAD задача может быть решена без столь громоздких
выкладок, а путём составления и решения системы уравнений, как это показано в
задаче 12.46.
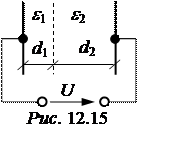
Задача 12.13. Какое максимальное напряжение можно подвести к двухслойному плоскому конденсатору рис. 12.15, если: ε1 = 2, ε2 = 4, d1 = = 2,5 мм, d2 = 5 мм. Пробивная напряженность изоляции: Епроб = 30 кВ/см. Запас электрической прочности принять равным n= 2,5.
 При найденном напряжении рассчитать объёмную плотность
энергии второго диэлектрика.
При найденном напряжении рассчитать объёмную плотность
энергии второго диэлектрика.
Решение
Исходя из принятого запаса электрической прочности, допустимая напряжённость поля в диэлектриках
Е1max £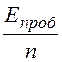 =
=![]() = 12 кВ/см, Е2max £
= 12 кВ/см, Е2max £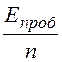 = 12 кВ/см.
= 12 кВ/см.
Если пренебречь краевым эффектом, то у плоского конденсатора напряжённость поля в каждой области постоянна – Е1 и Е2, соответственно. На границе раздела сред имеет место условие D1n = D2n, которое в данном случае приводит к выражению ε1E1 = ε2E2 или E1 = 2E2.
Так как E1 > E2, принимаем E1 = Е1max = 12 кВ/см.
Тогда E2 = ½E1 = 6 кВ/см.
Максимально допустимое напряжение на зажимах конденсатора
U= E1d1+ E2d2= 12·0,25 + 6·0,5 = 6 кВ.
Объёмная плотность энергии второго диэлектрика
w2 = ½ε2ε0E22 = 0,5·4·8,85·10 -14·60002 = 6,37·10 -6 Дж/см3.
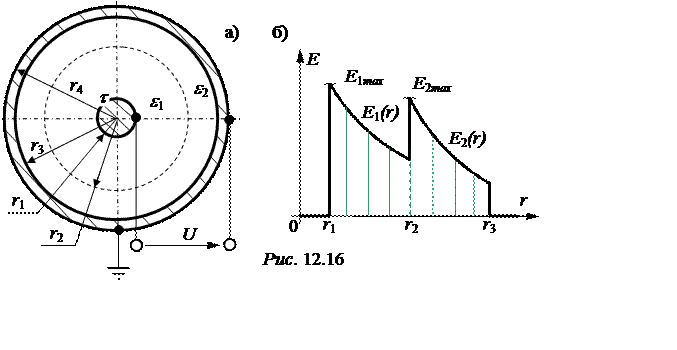
Задача 12.14. Какое максимальное напряжение можно подвести к двухслойному коаксиальному кабелю (рис. 12.16,a), если: r1 = 2,5 мм, r2 = = 7,5 мм, r3 = 12 мм, r4 = 14 мм, ε1 = 5, ε2 = 2. Пробивная напряженность изоляции: Е1проб = Е2проб = 30 кВ/см. Запас электрической прочности принять равным 3.
Вычислить ёмкость кабеля.
 |
При подключении кабеля к источнику постоянного напряжения Uжила кабеля будет нести на себе заряд tна единицу длины. Напряженность поля определим по (12.5).
Для первого слоя изоляции: Е1=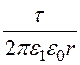 .
.
Для второго слоя: Е2=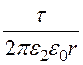 .
.
Качественная картина распределения напряженности приведена на рис. 12.16,б.
Наибольшая напряженность поля в слоях изоляции
Е1max =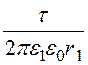 , Е2max=
, Е2max=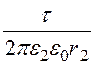 .
.
Чтобы не произошло пробоя изоляции:
Е1max≤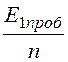 = 10 кВ, Е2max≤
= 10 кВ, Е2max≤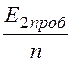 = 10 кВ.
= 10 кВ.
Произведения ε1r1 = 5·2,5 = 12,5; ε2r2 = 2·7,5 = 15; ε1r1 < ε2r2.
Поэтому Е1max> Е2max. Принимаем Е1max = 10 кВ.Тогда
τ = Е1max·2πε1ε0r1; Е1 =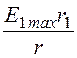 ; Е2 =
; Е2 =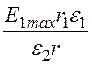 .
.
Напряжение первого слоя изоляции:
U1 = 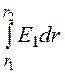 = Е1maxr1ln
= Е1maxr1ln![]() = 104·0,25ln3 = 2747 В;
= 104·0,25ln3 = 2747 В;
а
второго слоя: U2 = 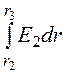 =
=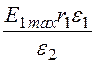 ln
ln![]() =
=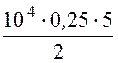 ln
ln![]() = 2937 В.
= 2937 В.
Максимальное рабочее напряжение кабеля:
 U= U1 + U2 = 2747 + 2937 = 5684 В.
U= U1 + U2 = 2747 + 2937 = 5684 В.
Заметим, что при изготовлении двухслойного коаксиального кабеля относительную диэлектрическую проницаемость изоляции внешнего слоя, как правило, нужно принимать меньшей, чем внутреннего слоя (ε2 < ε1). В противном случае (при ε1 < ε2) большая часть напряжения сети будет приложена к первому слою изоляции.
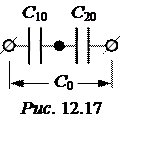
Емкость двухслойного кабеля (конденсатора) можно рассчитать, представив его последовательным соединением двух ёмкостей (рис. 12.17). В соответствии с (12.11) ёмкости слоёв и всего кабеля:
С10 =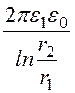 , С20 =
, С20 =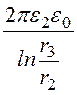 , С0 =
, С0 =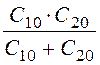 =
=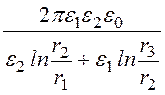 .
.
Или по определению ёмкости С0 =![]() =
=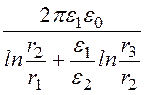 = 0,367 пФ/м.
= 0,367 пФ/м.
Задача 12.15. Максимальная напряжённость электростатического по-ля в изоляции двухслойного цилиндрического конденсатора (рис. 12.13, r = 0) составляет Еmax = 30 кВ/см. Требуется определить напряжение, приложен-ное к конденсатору, и его ёмкость, если
l = 5 м, e1 = 2, e2 = 1, r1 = 1 см, r2 = 3 см, r3 = 4 см и r4 = 5 см.
Решение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.