Коэффициенты akkи akm, зависящие от геометрических размеров тел, их взаимного расположения и свойств среды, в которой они находятся, имеют размерность [м/Ф] и являются положительными.
II группа формул Максвелла: t1 =b11j1 + b12j2 + b13j3 + …+ b1njn,
t2 = b21j1 + b22j2 + b23j3 + …+ b2njn,
- - - - - - - - - - - - - - - - - - - - - - - - - - tn=bn1j1 + bn2j2 + bn3j3 + …+ bnnjn.
В этих уравнениях bkm =![]() – емкостные коэффициенты, где
D – определитель системы I группы формул
Максвелла,
– емкостные коэффициенты, где
D – определитель системы I группы формул
Максвелла,
Dkm – алгебраическое дополнение.
Размерность ёмкостных коэффициентов [Ф/м].
III группа формул Максвелла: t1 = С11j1 + С12U12 + С13U13 + … + С1nU1n,
t2 = С21U21 + С22j2 + С23U23 + … + С2nU2n,
- - - - - - - - - - - - - - - - - - - - - - - - - - - tn = Сn1Un1 + Сn2Un2 + Сn3Un3 + … + Сnnj n, где Ukm – напряжение между проводами k и m.
Входящие в эти уравнения коэффициенты С называются частичными емкостями:
Ckk=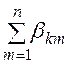 = bk1
+ bk2
+ … + bkk + … + bkn– собственная
частичная емкость,
= bk1
+ bk2
+ … + bkk + … + bkn– собственная
частичная емкость,
Ckm= -bkm– взаимная частичная емкость k-го и m-го проводников.
Размерность частичных ёмкостей [Ф/м].
 12.2. РАСЧЁТ ПОЛЯ С
ПОМОЩЬЮ ИНТЕГРАЛЬНЫХ СООТ-НОШЕНИЙ.
12.2. РАСЧЁТ ПОЛЯ С
ПОМОЩЬЮ ИНТЕГРАЛЬНЫХ СООТ-НОШЕНИЙ.Задача 12.1. Вывести формулы для опре-деления потока вектора электростатической индукции в функции координат а) от точечного заряда через сферическую поверхность радиуса R; б) от линейного заряда через цилиндрическую поверхность радиуса r.
Решение
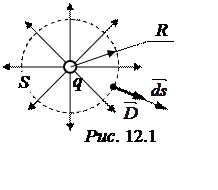
Для случая а) проведём вокруг точечного заряда q
сферическую поверхность S радиуса R (рис. 12.1) и применим
теорему Гаусса в интегральной форме: 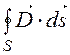 = Sq. Из определения
напряжённости поля вытекает, что силовые линии направлены радиально,
следовательно, перпендикулярно к поверхности S. Таким
образом, векторы
= Sq. Из определения
напряжённости поля вытекает, что силовые линии направлены радиально,
следовательно, перпендикулярно к поверхности S. Таким
образом, векторы ![]() и
и ![]() по
направлению совпадают, и их скалярное произведение можно заменить произведением
их модулей. Кроме того, значение вектора
по
направлению совпадают, и их скалярное произведение можно заменить произведением
их модулей. Кроме того, значение вектора ![]() во
всех равноудалённых от заряда q точках поверхности S одинаково
в силу симметрии; поэтому его можно вынести за знак интеграла. Таким образом,
получаем:
во
всех равноудалённых от заряда q точках поверхности S одинаково
в силу симметрии; поэтому его можно вынести за знак интеграла. Таким образом,
получаем:
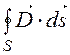 =
=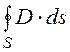 = D·
= D·![]() = D·S
= D·4p
·R2. (12.2)
= D·S
= D·4p
·R2. (12.2)
Следствие: индукция и напряженность поля точечного заряда –
D =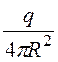 , Е =
, Е =![]() =
=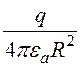 , (12.3)
, (12.3)
то есть зависят только от координаты R.
Аналогично поступим в случае б): проведём вокруг оси с
линейным зарядом t цилиндрическую поверхность S
радиуса r, длиной l и применим теорему Гаусса в
интегральной форме: 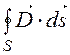 = Sq. В качестве иллюстрации можно
опять воспользоваться рис. 12.1, но после замены q на t и R на r, причем ось z направлена
перпендикулярно к плоскости рисунка. Предположим, что длина объекта значительно
больше его радиуса. Тогда можно пренебречь искажением плоскопараллельного поля
вблизи торцов цилиндра S и считать, что силовые линии направлены везде
радиально. В этом случае поток вектора
= Sq. В качестве иллюстрации можно
опять воспользоваться рис. 12.1, но после замены q на t и R на r, причем ось z направлена
перпендикулярно к плоскости рисунка. Предположим, что длина объекта значительно
больше его радиуса. Тогда можно пренебречь искажением плоскопараллельного поля
вблизи торцов цилиндра S и считать, что силовые линии направлены везде
радиально. В этом случае поток вектора ![]() через
торцовые части будет равен нулю, так как здесь угол между
через
торцовые части будет равен нулю, так как здесь угол между ![]() и
и ![]() составляет
90°. Во всех же точках боковой части векторы
составляет
90°. Во всех же точках боковой части векторы ![]() и
и ![]() по
направлению совпадают, и их скалярное произведение можно заменить произведением
их модулей. Кроме того, значение вектора
по
направлению совпадают, и их скалярное произведение можно заменить произведением
их модулей. Кроме того, значение вектора ![]() во
всех равноудалённых от оси z точках боковой части поверхности S
одинаково в силу симметрии; поэтому его можно вынести за знак интеграла. Таким
образом, получаем:
во
всех равноудалённых от оси z точках боковой части поверхности S
одинаково в силу симметрии; поэтому его можно вынести за знак интеграла. Таким
образом, получаем:
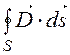 =
=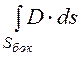 =
D·Sбок
= D·2p ·r·l.
(12.4)
=
D·Sбок
= D·2p ·r·l.
(12.4)
Следствие: индукция и напряженность поля заряженной оси –
 D
=
D
=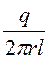 =
=![]() , Е
=
, Е
=![]() =
=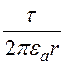 ,
(12.5)
,
(12.5)
то есть зависят только от координаты r.
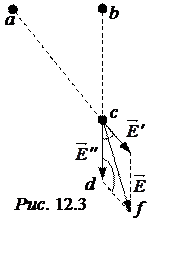 Задача 12.2.
Определить напряженность поля, создаваемого двумя зарядами в месте распо-ложения
третьего, и силу, действующую на
третий заряд, в системе точечных зарядов,
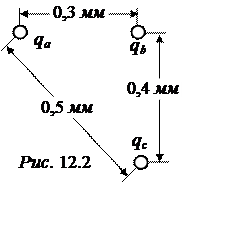
изображенной на рис. 12.2, где
Задача 12.2.
Определить напряженность поля, создаваемого двумя зарядами в месте распо-ложения
третьего, и силу, действующую на
третий заряд, в системе точечных зарядов,
изображенной на рис. 12.2, где
qa = 4·10-12 Кл, qb = 15·10-12 Кл, qc = 15·10-12 Кл.
Решение
Формула для напряженности электростатического поля, создаваемого уединённым точечным зарядом в вакууме, в соответствии с формулой (12.3) имеет вид:
E =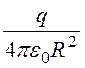 .
.
Тогда значения напряжённостей, создаваемых в точке с зарядами qa и qb будут, соответственно, равны (рис. 12.3):
E¢ =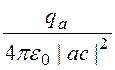 =
=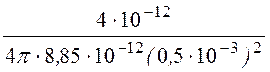 =
143,9·103 В/м = 143,9 кВ/м.
=
143,9·103 В/м = 143,9 кВ/м.
E¢¢ =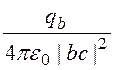 =
=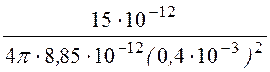 = 843,0·103 В/м = 843,0 кВ/м.
= 843,0·103 В/м = 843,0 кВ/м.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.