Электростатическое поле. Основные теоретические положения, страница 3

Определим угол при вершине с треугольника abс:

cos(Ðacb) = bс/ac = 0,4/0,5 = 0,8;    Ðacb = arccos 0,8 = 36,9°.

Тогда угол при вершине d треугольника cdf:

Ðcdf = 180° – 36,9° = 143,1°.

В соответствии с принципом наложения результирующий вектор искомой напряженности  равен векторной сумме   =¢+¢¢  (рис. 12.3). По теореме косинусов находим

Е ==

== 962 кВ/м.

Сила, действующая на заряд q_c, в соответствии с определением напря-женности электростатического поля равна:

F = q_c·E = 15·10^-12·962·10³ = 14,4·10^-6 Н.

Задача 12.3. Два шара с радиусами   R₁ = 0,2 см  и  R₂ = 0,5 см  находятся на расстоянии   d = 20 см  друг от друга в диэлектрике с относительной  проницаемостью  e = 4  (рис. 12.4).  Заряды шаров величиной  q = 10^-10 Кл  разного знака. Найти энергию поля и наибольшую напряженность.

Решение

Расстояние d значительно превышает радиусы шаров, поэтому можно считать, что геометрические и электрические центры шаров совпадают.

Между шарами напряжённости ¢ и ¢¢ складываются, а снаружи – вычитаются (рис. 12.4). Поэтому значение напряженности результирующего поля больше между шарами. С удалением от центра шара напряженность поля уменьшается, следовательно, максимальное значение напряженности нужно ожидать в точке на поверхности шара. Первый шар имеет меньший радиус (меньшее удаление от центра точек его поверхности), поэтому наибольшая напряженность поля будет в точке 1. Для расчёта поля в этой точке применим принцип наложения. На основании формулы (12.3)

Е₁ = Е₁¢ + Е₁¢¢ =+==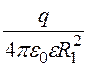

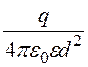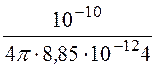
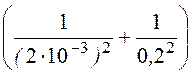= 56141 В/м.

Потенциал поля уединенного шара (аналогично задаче 12.5, формула 12.8):    j =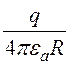+ А.

Если принять  j = 0  при  R = ¥,  то  А = 0.  Таким образом, потенциалы шаров равны

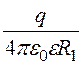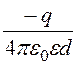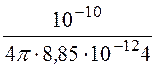
j₁ = j₁¢ + j₁¢¢ =+== 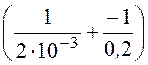111,1 В;

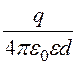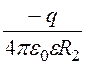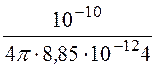
j₂ = j₂¢ + j₂¢¢ =+== 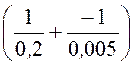-43,8 В.

Напряжение между шарами   U₁₂ = j₁ – j₂ = 111,1+ 43,8 = 154,9 В.

Ёмкость устройства                 C = q/U₁₂= 10^-10/154,9 = 0,645·10^-12 Ф.

Энергия поля            W_э = ½СU₁₂² = ½·0,645·10^-12·154,9² = 7,75·10^-9 Дж.

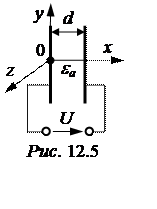
Задача 12.4. Вывести формулы для расчёта поля и ёмкости плоского конденсатора, у которого S – площадь пластин, d – расстояние между ними (рис. 12.5).

Решение

Площадь пластин S значительно больше квадрата расстояния d ² между ними. Поэтому поле между пластинами может считаться равномерным. Пусть заряд левой обкладки конденсатора имеет заряд q. Величина вектора электростатической индукции на основании граничного условия D = s = q/S. Напряжённость электрического поля  E = D/e_a = q/(S·e_a).  Приложенное напряжение   U = E·d = q·d/(S·e_a).   Емкость конденсатора

С = q/U = e_a·S/d.                                               (12.6)

Расположим оси декартовой системы координат, как показано на рис. 12.5. Пусть начало координат совмещено с левой пластиной. Получим формулу для потенциала j(х) на основании соотношения (12.1)   = -grad j.   В декартовой системе координат   grad j   представляется как

grad j =++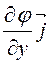  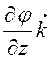 (см. табл. 11.1).

Очевидно, что потенциал  j  зависит только от одной координаты  х, то есть == 0; вектор  направлен вдоль оси  х, поэтому для его величины имеем: E = -. Отсюда

j = -= -Е·х + const.                           (12.7)

Если   конденсатор   имеет несколько слоёв, то емкость каждого слоя – С_k = e_ak·S/d_k, ёмкость всего конденсатора ввиду последовательного соединения емкостей слоёв  С = (S(С_k)^-1)^-1;  напряжение на каждом слое –  U_k = q/С_k; напряжённость поля в каждом слое –  E_k = U_k/d_k = q/(S·e_ak).

ЗАДАЧА 12.5. Получить формулы для расчёта поля и ёмкости шарового конденсатора, у которого внутренний и наружный радиусы диэлектрического слоя – r₁ и R₁, диэлектрическая проницаемость –  e_a  (рис. 12.6).

Решение

Пусть внутренний шар имеет заряд  q.  На основании формулы (12.3) электрическое смещение и напряжённость поля в диэлектрике

D = q/(4p ·R²);     Е = q/(4pe_a·R²).

Формулу для потенциала  j(R)  получим на основании соотношения (12.1).   В сферической системе координат   gradj   определяется как

gradj =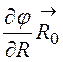++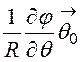  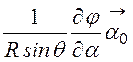 (см. табл. 11.1).