Простейшие приёмные антенны. Штыревая антенна радиоприемника (комнатная антенна)

15.2.3. Простейшие приёмные антенны

Задача 15.23. Штыревая антенна радиоприемника (комнатная антенна) представляет собой прямолинейный проводник длиной   l = 60 см, находящийся в воздухе, частота сигнала  f = 1 МГц  (диапазон средних волн). Действующее значение напряженности электрического поля в месте расположения антенны  Е = 4 мВ/м.

Расположить антенну так, чтобы в ней наводилась наибольшая ЭДС и рассчитать ее действующее значение.

Решение

Исходим из того, что приемная антенна находится в дальней зоне излучателя на расстоянии  R >> l, где  l – длина электромагнитной волны

l ==.

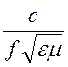Для воздушной среды рассматриваемого примера:    l =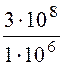= 300 м, что значительно больше линейного размера комнатной антенны длиной   l= 60 см, в связи с чем можно считать, что сигнал вдоль антенны имеет постоянную фазу.

На рис. 15.22 показаны направления векторов электромагнитной волны, распространяющейся вдоль координаты z.

Расположим антенну ОА в плоскости одинакового фазового состояния и рассчитаем индуктируемую в ней ЭДС

℮==.

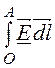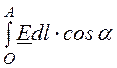Для получения максимальной ЭДС необходимо выполнить условие      a = 0,  совместив антенну ОА с осью ОХ декартовой системы координат. Значение максимальной ЭДС получим

℮_max= E·l= 4·0,6 = 2,4 мВ.

Задача 15.24. Штыревая антенна расположена в диэлектрике с отно-сительной диэлектрической проницаемостью  e= 4,   m = 1.  Длина антенны    l = 20 см,  частота сигнала  f = 2 МГц.  Действующее значение напряженности магнитного поля в месте расположения антенны   Н = 12 мкА/м.

Рассчитать максимальную ЭДС, индуктируемую в этой антенне.

Ответ.   45,2·10 ^-5 В.

Задача 15.25. Приемная антенна представляет собой прямоугольную рамку размерами  а= 30 см,  b= 15 см,  находящуюся в воздухе. Частота сигнала  f = 10⁷ Гц  (диапазон коротких волн). Действующее значение напря-женности магнитного поля в месте расположения рамки  Н = 80 мкА/м.

Найти наибольшую ЭДС, индуктируемую в рамке.

Определить наименьшую частоту, при которой можно применить эту рамку в качестве приемной антенны, если чувствительность приемника составляет  15 мкВ.

Решение

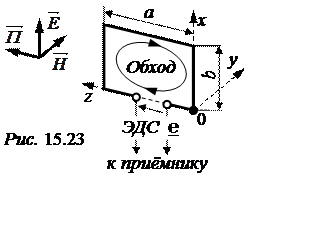
Для получения в рамке максимальной индуктированной ЭДС расположим рамку так, чтобы ее плоскость была параллельна направлению распространения волны, а вектор Н был бы перпендикулярен плоскости рамки (рис. 15.23).

Выберем для описания процесса декар-товую систему координат и поместим одну из вершин прямоугольной рамки в начало координат, а одну из сторон рамки совместим с осью 0х (рис. 15.23).

На основании решения волновых уравнений для плоской волны получаем:

Е= Е_х = Е₀е ^-jbz,   H= H_y=H₀е ^-jbz.

Примем, что при  z = 0   Н = H₀ = 80 мкА/м.

Волновое сопротивление воздушной среды:

Z_C=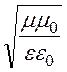==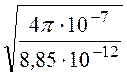 120p= 377 Oм.

Учитывая, что  Z_C=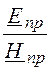=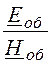, где сокращение пр – прямая волна, об – обратная волна, получаем значение напряженности электрического поля в начале координат

Е₀= H₀Z_C= 80·10 ^-6·377 = 30,16·10 ^-3 В/м.

Коэффициент распространения волны    p= jb,  причём  b = 2p/l.

Скорость распространения волны   v=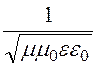= 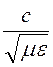  для воздуха равна скорости распространения света    v = c = 3∙10⁸ м/с.

Длина волны    l ===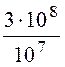 30 м,  b === 0,2094 рад/м.

При движении волны вдоль стороны aрамки приемной антенны изменение фазы колебания составляет       ba= 0,2094·0,3 = 0,0628 рад = 3,6°, если рамку повернуть на 90°, то получим  bb = 0,2094·0,15 = 0,0314 рад = 1,8°.

Наводимую ЭДС рассчитаем с помощью известного интегрального выражения  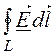 ℮ =, где интегрирование проводится по контуру рамки с направлением обхода контура, как указано на рис. 15.23 (согласовано с направлением вектора  правилом правоходового винта).

Если при    z = 0     Е = Е₀, то при  z = а   Е = Е₀e ^-jba, а индуктированная ЭДС   ℮ = bЕ₀e ^-jba – bЕ₀ = bЕ₀(e ^-jba – 1).

В рассматриваемом примере     ba= 0,0628 << 1, a

b ^-1 = 4,77 >> а = 0,3 м.

Для вычисления экспоненты и получения удобной формулы индуктируемой ЭДС воспользуемся разложением экспоненты в ряд

e ^x = 1 ++++ …

В нашем примере третье слагаемое составляет малую часть второго:

:== ½ba= 0,0314,  т.е. 3% от второго.

Поэтому с достаточной степенью точности  e ^-jba = 1 – jba,  а индукти-руемая в антенне ЭДС

℮= -jbabЕ₀ = -jwmm₀ab= -jwmm₀abH₀ = -jwabB₀ = -jwФ₀, где Ф₀ – магнитный поток рамки, если по ее площади можно считать магнитную индукцию неизменной и равной  B₀ = mm₀H₀, т.е. рассчитанную через напряженность поля при  z = 0.

Комплексное значение ЭДС

℮= -j0,0628·0,15·30,16 = -j0,284 мВ.

Заметим, что при повороте рамки вокруг оси 0у на 90° расчетная приближенная формула не изменится и по-прежнему  ℮ = -jbabЕ₀  – индук-тируемая ЭДС обратно пропорциональна длине волны, а следовательно, пропорциональна частоте.

Поэтому минимальная частота, при которой указанную рамку можно применять как приемную антенну для приемника с чувствительностью       ℮_min = 15 мкВ

f_min = ℮_minf/℮ =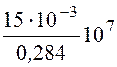 = 0,53·10 ⁶ Гц = 0,53 МГц.

Задача 15.26. Прямоугольный контур со сторонами  а = 10 см,   b =  = 20 см  расположен в поле бегущей синусоидальной волны так, что плос-кость его перпендикулярна вектору , а две стороны  а  совпадают по направлению с вектором . Частота сигнала  f = 2∙10⁷ Гц, окружающая среда – немагнитный диэлектрик с  e = 4.