Если kz – величина мнимая, то это означает, что волна вдоль волновода не распространяется, а электромагнитное поле, изменяясь гармонически в каждой точке волновода, затухает экспоненциально вдоль волновода без переноса энергии.
Для существования волнового процесса необходимо, чтобы
![]() kz2 > 0 или
kz2 > 0 или 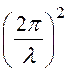 –
–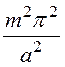 –
–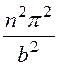 > 0.
> 0.
Отсюда получаем граничную длину волны (критическую)
λкр =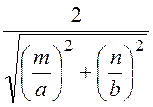 , а
передача энергии по волноводу возможна при λ < λкр.
, а
передача энергии по волноводу возможна при λ < λкр.
Окончательное выражение для векторного магнитного потенциала ТМmn волны
A= Az = Dsin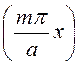 sin
sin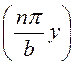
![]() .
.
Заметим, что при m = 0 или n = 0 A= 0 и все проекции векторов Н и Е равны нулю. Поэтому наименьшие значения m = 1, n = 1 и самая простая ТМ волна обозначается как ТМ11.
Формулу для расчета коэффициента распространения волны вдоль волновода можно представить в другом виде, имея соотношение для λкр
kz2 =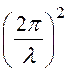 – p 2
– p 2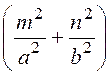 , откуда kz =
, откуда kz =![]()
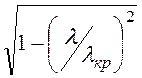 , длина
волны в этом волноводе L =
, длина
волны в этом волноводе L =![]() =
=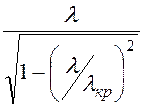 >
λ, а
фазовая скорость vф =
Lf=
>
λ, а
фазовая скорость vф =
Lf=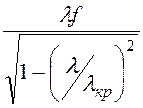 =
=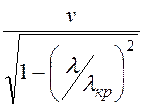 .
.
Для воздуха v = c = 3∙108 м/с и vф > c.
Волновое сопротивление волновода определяется составляющими напряженностей в поперечном направлении волновода. Они разные для волн ТМ и ТЕ.
Для волны ТМ
ZCTM =![]() =
=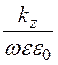 =
=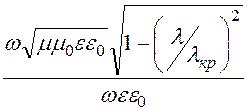 = ZC 0
= ZC 0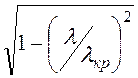 , где
ZC 0=
, где
ZC 0=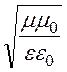 – волновое
сопротивление свободного пространства.
– волновое
сопротивление свободного пространства.
ЗАДАЧА 15.38. Какого типа поперечные магнитные волны можно создать в прямоугольном волноводе, заполненном воздухом, с размерами а = 2,5 см; b= 5 см при частоте f= 7,5∙109 Гц?
Найти значение критической длины волны и длины волны в волноводе в каждом случае.
Ответ: ТМ11, λкр = 4,47 см,L= 8,95 см.
ЗАДАЧА15.39. Действующее значение продольной составляющей напряженности электрического поля в центре сечения волновода задачи 15.38 составляет 105 В/м.
Определить действующие значения поперечных составляющих электрического и магнитного полей волновода в этом сечении.
Рассчитать передаваемую по волноводу мощность.
Решение
При решении задачи 15.37 получено Ez=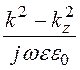 A, откуда осевое значение векторного магнитного
потенциала волновода
A, откуда осевое значение векторного магнитного
потенциала волновода
A =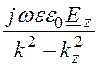 = j
= j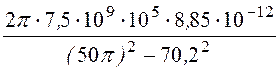 = j2,11 A, где k = w
= j2,11 A, где k = w ![]() =
=![]() =
=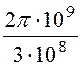 = 50pрад/м,
= 50pрад/м,
kz =![]()
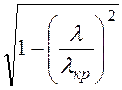 =
=![]()
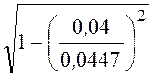 = 70,2 рад/м,
= 70,2 рад/м,
λ =![]() =
=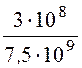 = 0,04 м.
= 0,04 м.
Если начало отсчета выбрать в соответствии с рис. 15.28, то нами рассчитано численное значение потенциала для точки с координатами x0 = ½а = 0,0125 м,y0 = ½b = 0,025 м,z0 = 0, а векторный потенциал определяется выражением
A=
Az(x, y, z) = Dsin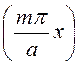 sin
sin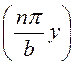
![]() .
.
В нашем примере m= 1, n= 1, ![]() x0 = ½p рад,
x0 = ½p рад, ![]() y0 = ½p рад, а полученное численное значение A
y0 = ½p рад, а полученное численное значение A
A= Dsin(½p)sin(½p) = D = j2,11 A.
Поперечные составляющие магнитного поля прямоугольного волновода с волной типа ТМmn
Hx =![]() = D
= D![]() sin
sin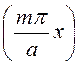 cos
cos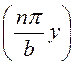
![]() ,
,
Hy = -![]() = -D
= -D![]() cos
cos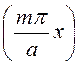 sin
sin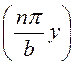
![]() , поперечные
составляющие электрического поля
, поперечные
составляющие электрического поля
Еx =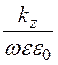 Hy = -D
Hy = -D![]()
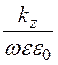 cos
cos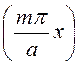 sin
sin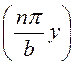
![]() ,
,
Еу = -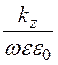 Hх
= -D
Hх
= -D![]()
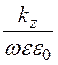 sin
sin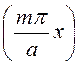 cos
cos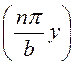
![]() .
.
Подставляя числа, получаем
Hx = j132,6sin(40px)·cos(20py)e –j70,2z A/м,
Hy = -j265cos(40px)·sin(20py)e –j70,2z A/м,
Еx = -j44,6·103cos(40px)·sin(20py)e –j70,2z B/м,
Еy = -j22,32·103sin(40px)·cos(20py)e –j70,2z B/м.
Передаваемая по волноводу активная мощность
P= Im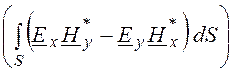 =
=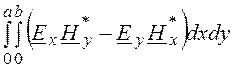 .
.
При подсчете учтем, что при m и nцелых числах
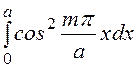 =½a,
=½a,
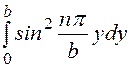 =½b,
=½b, 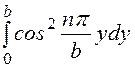 =½b,
=½b, 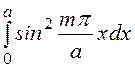 =½a.
=½a.
Получим
P =
(265·44,6·103 + 22,32·103·132,6)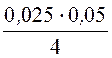 = 4,62·103 Вт =
4,62 кВт.
= 4,62·103 Вт =
4,62 кВт.
ЗАДАЧА 15.40. Амплитудное значение продольной составляющей напряженности электрического поля в центре сечения прямоугольного волновода размерами 2,5´5 см 2 составляет 105 В/м. Частота 9∙109 Гц. Тип волны ТМ12. Диэлектрик – воздух. Определить мощность, передаваемую по волноводу.
Ответ: P= 1,56 кВт.
ЗАДАЧА 15.41. В прямоугольном волноводе с размерами поперечного сечения а и bи с неограниченным продольным размером поле возбуждается рамкой с током, магнитный момент которой совпадает с направлением оси волновода.
Вывести общие выражения для составляющих электромагнитного поля в волноводе. Определить тип волны. Составить формулы для критической длины волны, фазовой скорости, характеристического сопротивления и передаваемой мощности.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.