ЗАДАЧА 15.35.
Магнитный излучатель (рамочная антенна) представля-ет собой круглый виток
тонкого провода радиусом а = 2 см,
расположенный в воздухе. Вдоль витка протекает синусоидальный ток i =
2![]() sin(ωt+
60°) A
частоты f = 2∙108
Гц. Виток расположен в экваториальной плоскости сферической системы
координат, его центр лежит в начале координат.
sin(ωt+
60°) A
частоты f = 2∙108
Гц. Виток расположен в экваториальной плоскости сферической системы
координат, его центр лежит в начале координат.
 Определить комплексы векторов напряженностей
электрического и магнитного полей в точке М(10 м; 30°; 90°).
Определить комплексы векторов напряженностей
электрического и магнитного полей в точке М(10 м; 30°; 90°).
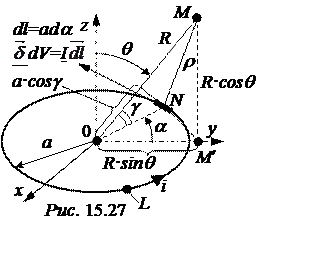
Представим картинку расположения витка рамочной
антенны и точки наблюдения М на рис. 15.27, где R– расстояние
от центра антенны до точки наблюдения, r – расстояние от
произвольно-го элемента тока I![]() до точки наблюдения. Координаты элемента тока N(а; ½p; a),
координаты точки наблюдения М(R; q; 0) – точку наблюдения мы расположили в плоскости z0y,
за начало отсчета координаты a принято направление оси y.
до точки наблюдения. Координаты элемента тока N(а; ½p; a),
координаты точки наблюдения М(R; q; 0) – точку наблюдения мы расположили в плоскости z0y,
за начало отсчета координаты a принято направление оси y.
Рассчитаем векторный электродинамический потенциал рамочной антенны для точки наблюдения:
![]() =
=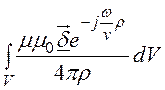 =
=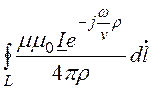 .
.
Произвольный элемент тока I![]() =Iada определяет элементарное слагаемое векторного потенциала
=Iada определяет элементарное слагаемое векторного потенциала
d ![]() =
=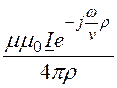 a·cosada
·
a·cosada
·![]() , имеющее
только одно направление – вдоль координаты a принятой сферической системы координат. Эту же проекцию имеет и
результирующий вектор
, имеющее
только одно направление – вдоль координаты a принятой сферической системы координат. Эту же проекцию имеет и
результирующий вектор ![]() =
=![]() A, и эта проекция
A, и эта проекция
A =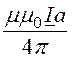
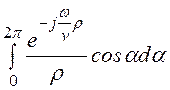 .
.
Предположим, что точка наблюдения М, для которой определяется векторный электродинамический потенциал, находится на очень большом расстоянии от антенны так, что a << R. В этом случае для знаменателя можно принять r = R. Однако для показателя экспоненты отличие r от Rможет привести к заметной ошибке по фазе волны.
В рассматриваемом случае
r» R – a·cosg
= R – a·sinqcosa,5)
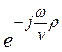 »
» 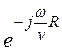
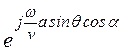 .
.
Заметим, что ![]() =
=![]() , тогда
, тогда ![]() a =
a =![]() а,что при соотношении
а,что при соотношении ![]() >>aприводит к
>>aприводит к ![]() а
<< 1 и при разложении экспоненты в ряд достаточно учесть два первых
члена разложения
а
<< 1 и при разложении экспоненты в ряд достаточно учесть два первых
члена разложения 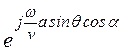 » 1 + j
» 1 + j![]() a·sinqcosa
a·sinqcosa
и
векторный потенциал A =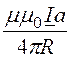
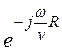
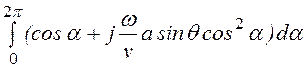 .
.
Так как 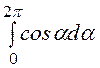 = 0, а
= 0, а
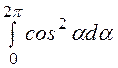 =
=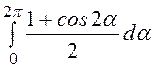 = p, то оконча-тельное выражение для векторного
потенциала приобретает вид
= p, то оконча-тельное выражение для векторного
потенциала приобретает вид
A =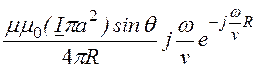 .
.
Учтем, что произведение тока I на площадь πа2,охваченную контуром с током есть магнитный момент контура m = IS= Iπа2.
Тогда формулу для расчета векторного потенциала можно
представить в векторной форме ![]() =
=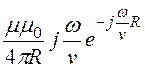
![]() .
.
Вектор напряженности магнитного поля вычислим с
помощью соотношения ![]() =
=![]() rot
rot![]() .
.
В сферической системе координат с учетом ![]() =
=![]() A и A = f(R,
q)
A и A = f(R,
q)
rot![]() =
=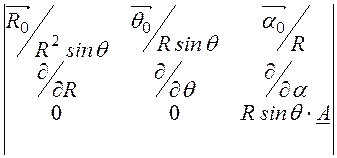 =
=
=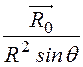
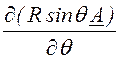 –
–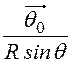
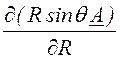 =
=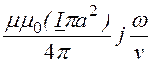 ´
´
´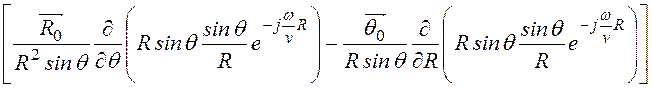 =
=
=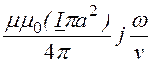
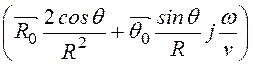 .
.
Таким образом, вектор напряженности магнитного поля имеет две проекции:
HR =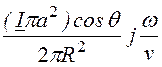
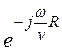 = j
= j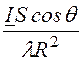
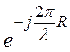 , (1)
, (1)
Hq =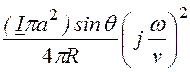
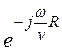 = -
= -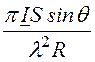
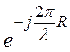 . (2)
. (2)
Вектор напряженности электрического поля вычислим с
помощью соотношения: ![]() =
=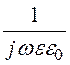 rot
rot![]() ,
где
,
где
rot![]() =
=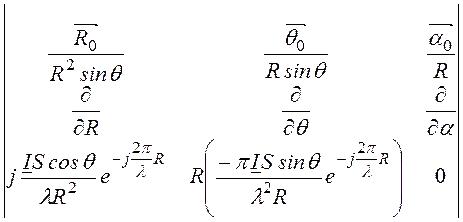 =
=
=![]()
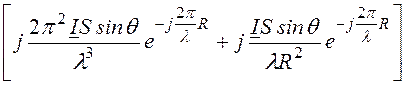 .
.
Таким образом,
![]() =
=![]()
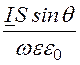
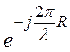
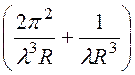 –
вектор напряженности электрического поля имеет одну проекцию в
сферической системе координат. Последнему выражению можно придать
другую редакцию:
–
вектор напряженности электрического поля имеет одну проекцию в
сферической системе координат. Последнему выражению можно придать
другую редакцию:
E = Ea =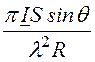 ZC
ZC 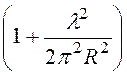
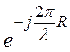 , где ZC =
, где ZC =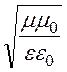 . (3)
. (3)
Для дальней зоны излучателя получаем: HR = 0,
H = Hq = -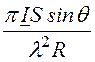
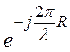 , E = Ea =
, E = Ea =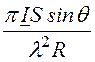 ZC
ZC 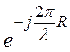 , а
отношение
, а
отношение ![]() = ZC (знак «минус»
в выражении для H соответствует
принципу излучения).
= ZC (знак «минус»
в выражении для H соответствует
принципу излучения).
Для рассматриваемой задачи
λ =![]() =
=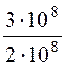 =1,5 м; I =
=1,5 м; I =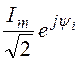 = 2e j60° A; S= pa2 = p ·(2·10 -2)2 =12,56·10 -4 м2.
= 2e j60° A; S= pa2 = p ·(2·10 -2)2 =12,56·10 -4 м2.
Начало отсчета координаты a совместим с положительным направле-нием оси x декартовой системы координат. Для точки М(10 м; 30°; 90°) получаем в соответствии с (1)-(2):
HR = j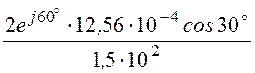 e j120° =
14,5·10 -6e –j90° A/м, где
e j120° =
14,5·10 -6e –j90° A/м, где ![]() R =
R =![]() ·10 = 2p ·6,67 = 41,9 рад,e –j41,9рад = e +j120°;
·10 = 2p ·6,67 = 41,9 рад,e –j41,9рад = e +j120°;
Hq = -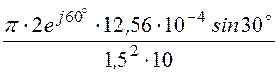 e j120° =
1,754·10 -4 A/м.
e j120° =
1,754·10 -4 A/м.
По модулю H=![]() = 1,76·10
-4 A/м, что практически соответ-ствует дальней зоне
излучения.
= 1,76·10
-4 A/м, что практически соответ-ствует дальней зоне
излучения.
При расчёте напряжённости электрического поля
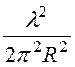 =
=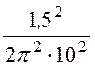 =0,00114, что также
соответствует дальней зоне излучения.
=0,00114, что также
соответствует дальней зоне излучения.
Тогда E = Ea = ZC(-Hq ) = 377·(-1,754·10 -4) = -0,0651 В/м.
Задача 15.36. Вывести формулы для расчета мощности излучения Р и сопротивления излучения rрамочной антенны. Вычислить Р и rдля условий задачи 15.35.
Решение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.