Имея в виду целью расчета определение зависимости ![]() , удобно вво-дить магнитный векторный
потенциал
, удобно вво-дить магнитный векторный
потенциал ![]() так, чтобы
так, чтобы ![]() = rot
= rot![]() (задачи 15.37 и 15.39). Этот векторный
потенциал в mm0 раз
меньше ранее рассмотренного и отличается от него размерностью (измеряется в
амперах).
(задачи 15.37 и 15.39). Этот векторный
потенциал в mm0 раз
меньше ранее рассмотренного и отличается от него размерностью (измеряется в
амперах).
Он удовлетворяет векторному уравнению Ñ 2![]() –
–![]()
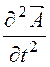 =
-
=
-![]() или в комплексной форме Ñ 2
или в комплексной форме Ñ 2![]() +
+![]()
![]() = -
= -![]() , соответственно, при
, соответственно, при ![]() = 0 – волново-му уравнению Ñ 2
= 0 – волново-му уравнению Ñ 2![]() –
–![]()
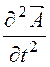 = 0 или в комплексной форме Ñ 2
= 0 или в комплексной форме Ñ 2![]() +
+![]()
![]() =
0.
=
0.
Уравнения связи принимают вид:
div![]() = -ee0
= -ee0![]() илиdiv
илиdiv![]() =
-jwee0j 0,
=
-jwee0j 0,
![]() = -mm0
= -mm0![]() – grad j или
– grad j или ![]() = -jwmm0
= -jwmm0![]() – grad j , магнитный
потенциал элемента синусоидального тока
– grad j , магнитный
потенциал элемента синусоидального тока ![]() =
=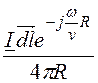 .
.
Заметим, что в свободном пространстве при отсутствии
токов проводимости d = 0 и свободных зарядов ![]() r= 0 и
однородной изотропной среде уравнения Максвелла принимают вид как в табл. 15.5.
r= 0 и
однородной изотропной среде уравнения Максвелла принимают вид как в табл. 15.5.
Таблица 15.5
|
Для мгновенных значений |
В комплексной форме |
|
rot div |
rot div |
Отсутствие истоков у вектора ![]() в
этой области указывает на его соленоидный характер, и для его расчета можно
ввести электрический векторный потенциал поля
в
этой области указывает на его соленоидный характер, и для его расчета можно
ввести электрический векторный потенциал поля ![]() так,
чтобы rot
так,
чтобы rot![]() =
=![]() .
.
Одновременно вводится скалярный потенциал магнитного поля jм.
Четыре уравнения Максвелла при этом сводятся к одному из двух волновых уравнений
1) Ñ 2![]() – mm0ee0
– mm0ee0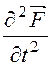 = 0 или Ñ 2
= 0 или Ñ 2![]() +
+![]()
![]() = 0;
= 0;
2) Ñ 2jм – mm0ee0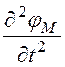 = 0 или Ñ 2jм +
= 0 или Ñ 2jм +![]() jм =
0;
jм =
0;
а уравнения связи принимают вид:
div![]() = mm0
= mm0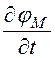 или div
или div![]() =
-jwmm0jм,
=
-jwmm0jм,
![]() = -grad j м + ee0
= -grad j м + ee0![]() или
или ![]() = -grad j м + jwee0
= -grad j м + jwee0![]() .
.
 15.3.1. Излучение энергии электромагнитного поля
простейшими излучающими антеннами
15.3.1. Излучение энергии электромагнитного поля
простейшими излучающими антеннами
ЗАДАЧА 15.30. В излучающей антенне проходит переменный ток частотой f = 5 МГц. Рассматривая антенну как эквивалентный диполь длиной l= 10 м, заряд которого в Кулонах q= 3∙10-7sinwt (рис. 15.25), найти напряженности магнитного и электрического по-лей в точках прямой, исходящей из центра диполя под углом 40° к горизонту, на расстояниях от центра диполя: а) 30 м; б) 5 км.
Решение
Векторный потенциал для прямолинейного отрезка с синусоидальным током
A =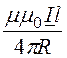
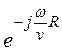 .
.
Мгновенное значение тока
i
=![]() = 3·10-7·2p ·5·106·cos wt = 9,425cos wt A, комплекс
тока I =
= 3·10-7·2p ·5·106·cos wt = 9,425cos wt A, комплекс
тока I =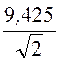 e j90° = j6,67 A.
e j90° = j6,67 A.
Векторный потенциал диполя совпадает по направлению с вектором плотности тока и в соответствии с рис. 15.25 имеет единственное направление на полюс сферической системы координат, то есть только две проекции по координатам:
AR = Acosq =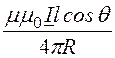
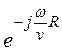 , Aq = -Asinq = -
, Aq = -Asinq = -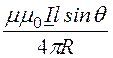
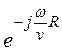 .
.
фазовая скорость распространения волны в воздухе v
= c = 3·108 м/c, длина
волны l =![]() =
=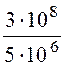 = 60 м.
= 60 м.
Напряженность магнитного поля дипольной антенны
определим из формулы ![]() =
= ![]() rot
rot![]() .
.
В рассматриваемой задаче
rot![]() =
=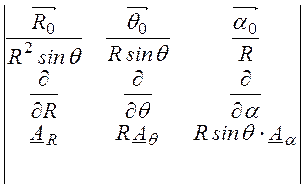 =
=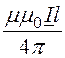
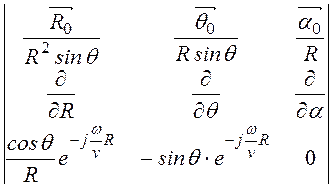 =
=
=![]()
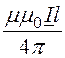 ·
·![]()
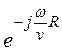 sinq ·
sinq ·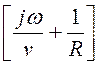 .
.
Таким образом, вектор ![]() имеет
только одну проекцию:
имеет
только одну проекцию:
H = Ha =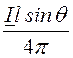
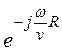
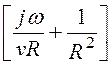 .
.
На основании первого уравнения Максвелла ![]() =
= 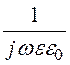 rot
rot![]() .
.
В нашей задаче
rot![]() =
=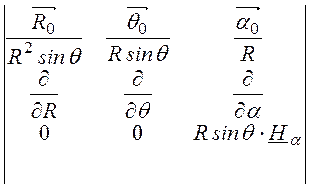 =
=
=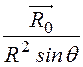 ·
·![]()
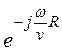
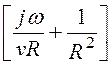 R
R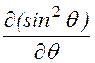 –
–
–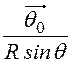
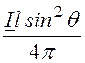
![]()
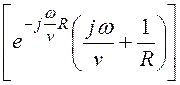 =
=
=![]()
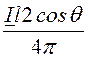
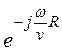
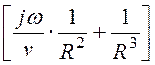 –
–
–![]()
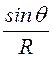
![]()
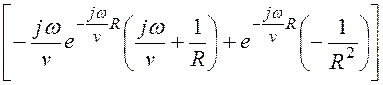 .
.
Таким образом, вектор напряженности электрического поля имеет две проекции:
ER =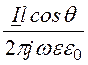
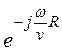
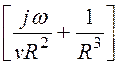 , Eq =
, Eq =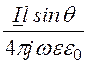
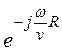
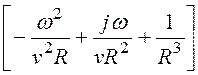 .
.
Учтем, что ![]() =
=![]() .
.
Тогда выражения для напряженностей можно представить в виде:
H = Ha =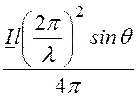
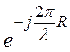
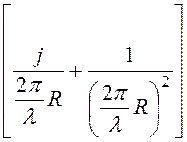 , (1)
, (1)
ER =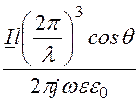
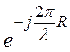
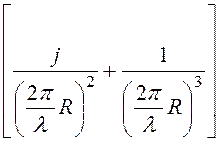 ,
(2)
,
(2)
Eq =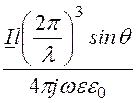
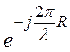
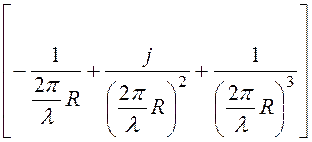 . (3)
. (3)
Обратим внимание на произведение 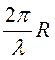 , стоящее в знаменателях слагаемых, заключенных
в квадратные скобки:
, стоящее в знаменателях слагаемых, заключенных
в квадратные скобки:
1)
если 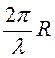 =
1 или R =
=
1 или R =![]() (в рассматриваемом примере λ = 60 м,
R=
=
(в рассматриваемом примере λ = 60 м,
R=
=![]() ≈ 5 м ≈ 0,1λ), то
все слагаемые одинаковы по модулю; пространство на таком расстоянии от
излучающей антенны называют зоной неуверенного приема;
≈ 5 м ≈ 0,1λ), то
все слагаемые одинаковы по модулю; пространство на таком расстоянии от
излучающей антенны называют зоной неуверенного приема;
2)
если 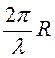 =
100, то каждое следующее слагаемое в выражениях для напряженностей в 100 раз
меньше предыдущего, их можно опустить, допустив погрешность расчета
напряженностей около 1% (в примере это R≥ 500 м). Это – дальняя
зона излучателя;
=
100, то каждое следующее слагаемое в выражениях для напряженностей в 100 раз
меньше предыдущего, их можно опустить, допустив погрешность расчета
напряженностей около 1% (в примере это R≥ 500 м). Это – дальняя
зона излучателя;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.