Простейшие приёмные антенны. Штыревая антенна радиоприемника (комнатная антенна), страница 2

Действующее значение напряженности магнитного поля в месте расположения рамки   Н = 0,4 мА/м. Найти ЭДС, индуктируемую в контуре, двумя способами: а) ℮ =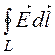,   б) ℮ = -.

Ответ:   ℮ = |Z_CНb(e ^-jba – 1)| = 1,263 мВ.

ЗАДАЧА 15.27. Круглый виток диаметром  d = 20 cм  находится в воздухе с электромагнитным полем частоты  f = 1 МГц.

Напряженность электрического поля (действующее значение) в центре расположения витка   Е₀ = 100 мкВ/м.   Расположить виток так, чтобы наводимая в нем ЭДС была максимальной. Определить действующее значение этой ЭДС.

Решение

Для получения максимальной наводимой в приемной антенне ЭДС виток необходимо расположить так, чтобы его плоскость была перпендикулярна вектору Н плоской электромагнитной волны (рис. 15.24).

Длина электромагнитной волны в воздухе          l===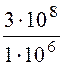 300 м.

Комплекс напряженности магнитного поля бегущей волны:

Н= A.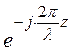

При перемещении волны вдоль плоскости витка на расстояние  dфаза волны изменится на величину

d=·0,2 = 0,0042 рад = 0,24 град.

Это очень малая величина, поэтому будем считать, что комплекс напряженности магнитного поля по площади S приемной антенны постоянен:

Н₀=== 0,265 мкА/м.

Наибольшее значение индуктируемой ЭДС

℮ = wФ = 2pfm₀Н₀S= 2pfm₀Н₀= 2p ·10⁶·4p ·10 ^-7·0,265·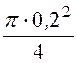= 0,0656 мкВ.

Задача 15.28. Плоскость контура расположена:

а) перпендикулярно к направлению движения бегущей плоской электромагнитной волны;

б) перпендикулярно вектору Е;

в) перпендикулярно вектору Н.

В каком из этих трех случаев в контуре будет индуктироваться ЭДС?

Обоснуйте ответ.

ЗАДАЧА 15.29. Антенна выполнена из ферритового стержня сечением S = 0,25 см²  и имеет в средней части катушку с числом витков  w = 50. Сред-няя магнитная проницаемость стержня m = 160. Напряженность электриче-ского поля в месте расположения антенны  Е₀ = 30 мВ/м.

Определить наибольшее значение ЭДС, наводимой в катушке, если частота работы передающей станции   f= 600 кГц.

Ответ: ℮ = wmm₀Sw = 75,3 мкВ, где Z_C=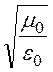= 377 Ом – волновое сопротивление воздуха.

15.3. ЭЛЕКТРОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ ЭЛЕКТРО-МАГНИТНОГО ПОЛЯ И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С НИМИ

Задача расчета состояния электромагнитного поля в основном сводится к определению законов изменения векторов  и  этого поля как функций времени и координат.

В простых случаях, рассмотренных ранее, эти векторы определялись на основании непосредственного решения уравнений Максвелла, в более слож-ных случаях расчеты удобнее производить с помощью вспомогательных функ-ций: 1) векторного потенциала поля ;  2) скалярного потенциала поля j.

Для однородной изотропной среды, когда характеристики среды g, e, mнеизменны по всем направлениям и не зависят от времени, четыре уравнения Максвелла сводятся к одному уравнению Даламбера

векторному Ñ ² – 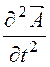= -mm₀  или скалярному  Ñ ²j –= -.

В этих уравнениях  v =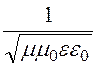=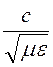,  где  с =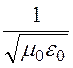= 3·10⁸ м/с – электромагнитная постоянная, равная скорости света (скорость распространения электромагнитных волн в пустоте).

Основные векторы поля связаны с электродинамическими потенциалами соотношениями:

= rot,   =rot,   = - – grad j, а потенциалы связаны зависимостью   div= -.

В комплексной форме получаем:

= rot,   mm₀=,   = -jw – grad j ,div= -j ,

Ñ ²+= -mm₀,    Ñ ²j +j = -.

Вне проводящей среды  g = 0,  d =gЕ = 0  и при отсутствии свободных зарядов  r= 0  уравнения Даламбера превращаются в волновые уравнения

Ñ ²+= 0,    Ñ ²j +j = 0.

Решения уравнений Даламбера, представленных в комплексной форме,

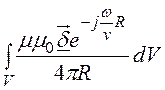 =,     j =.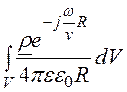

Заметим, что  k== называют волновым числом, а l – длина волны в данной среде.

Поскольку  dV = S·dl,  где S – поперечное сечение тонкого проводника, то элемент тока     i=··=dV.

Векторный потенциал элемента синусоидального тока

 =.

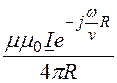
Для однородной изотропной среды при m = constиз  div= 0  с учетом = mm₀ получаем   div= 0.