Простейшие приёмные антенны. Штыревая антенна радиоприемника (комнатная антенна), страница 4

3)  если 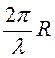  = 0,01   (в примере  R< 0,05 м) – это ближняя зона излучателя, напряженности с погрешностью ≈1% определяются только слагаемым 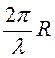 в старшей степени.

Для количественного определения параметров напряженностей в соответствии с рис. 15.25 определяем координату   q= 90° – 40° = 50°.

Для заданного случая  а)  R= 30 м  иl= 60 м  по (1) с учетом

== 0,1047 рад/м = 6 град/м     и R= 0,1047·30 = 3,14

H =H_a=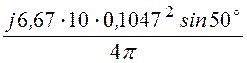e^-j6°·30·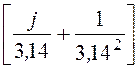= 0,015e^-j17,5° A/м,

E_R =e^-j180°·=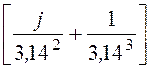

= 28,2e^-j180°·(j0,101 + 0,032) = 2,995e^-j107,7° B/м,

E_q =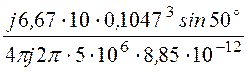e^-j180°·=

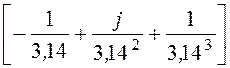= 16,79e^-j180°·(j0,101 – 0,286) = 5,094e^-j19,5° B/м.

Для заданного случая  б)  R= 5000 м

R = 0,1047·5000 = 83,33·2p рад = 523,6 рад = 30°·10³.

Это – дальняя зона излучателя, и при расчете напряженностей учитываются только первые слагаемые выражений (1)-(3). Отбросив целое число периодов (83), получим 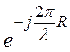  = e^-j120°.

Таким образом, для дальней зоны

H =H_a=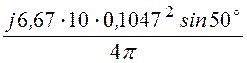e^-j120°· А/м = -85,1e^-j120° мкА/м,

E_R = 0,

E_q = 16,93e^-j120°·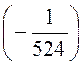B/м = -32,3e^-j120°мB/м.

ЗАДАЧА 15.31. Для условий задачи 15.30 рассчитать скалярный электродинамический потенциал  j  электромагнитного поля.

Решение

Скалярный электродинамический потенциал рассчитаем по уравнению связи между векторным и скалярным потенциалами в комплексной форме:

div= -j .

Так как в данном случае  не зависит от координаты a, то в сферической системе координат

div =(R²A_R) +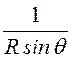(sinq ·A_q ).

Подставим полученные при решении задачи 15.30 выражения для проекций векторного электродинамического потенциала прямолинейной антенны и выполним операции дифференцирования. Тогда

div=+=

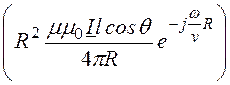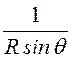
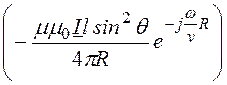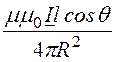
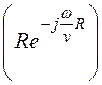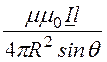
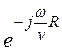
=–(sin²q ) =

=.

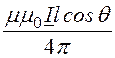
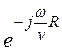
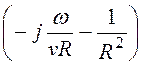Подставим это выражение в уравнение связи и получим

j = -div==

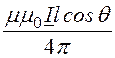
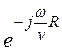
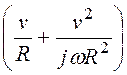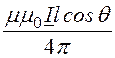
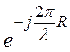=w .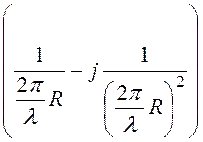

Для случая  а)  R= 30 м и λ = 60 м получаем

j ==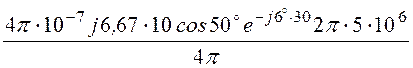

= 134,7e^-j90°·(0,318 – j0,101) = 44,99e^-j107,7° B.

Для случая  б) R= 5000 м  получаем (исключая целое число периодов)

j =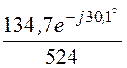= 0,257e^-j30,1° B.

ЗАДАЧА 15.32. Рассчитать мощность излучения и сопротив-ление излучения антенны задачи 15.30.

Решение

Для определения мощности излучения прямолинейной антен-ны в дальней зоне излучения проведем сферическую поверх-ность радиусом R, в центре которой находится излучатель (рис. 15.26) и вычислим поток комплексного вектора Пойнтинга через эту сферу. На поверхности сферы в дальней зоне

H = H_a =,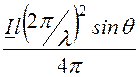

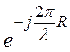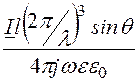
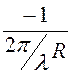
E_R = 0,      тогда     E = E_q =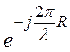, комплексный вектора Пойнтинга

П = П_R = E_q ==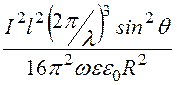 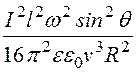–  действительное число.

Поток мощности излучения через сферическую поверхность 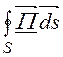 ,  где  ds= 2p ·Rsinq ·Rdq= 2p ·R²sinq ·dq,   а векторы    и    совпадают по направлению.

Так как  П – действительное число, то излучается активная мощность

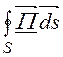P==·2p .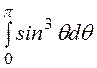

Представим   sin³q  = ¾sinq – ¼sin3q,  тогда

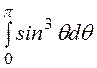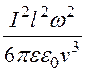= -cosq +cos3q =+––=,  а   P=.     (4)

Для расчета мощности излучения формуле (4) можно придать другое выражение, пригодное для любой среды:

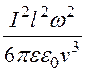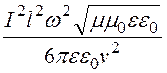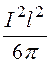
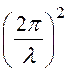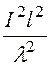P===·Z_C =··Z_C.

Для воздуха   Z_C =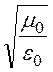= 120p = 377 Ом,  тогда   P= 80p ²·I ².

Сопротивление излучателя чисто активное

r==Z_C,    а для воздуха   r= 80p ².

Для условий задачи 15.30 –l = 10 м,  λ = 60 м,I = 6,67 A–

Р = 80p ²·6,67 ²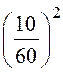= 976 Вт,    r= 80p ²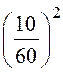= 21,93 Ом.

ЗАДАЧА 15.33. Вдоль отрезка провода длиной   l= 10 см  протекает синусоидальный ток частоты   f= 3∙10⁷ Гц.   Известно, что в точке А, сферические координаты которой  R_A = 100 м, q_A = 90°,  a_A = 30°,  вектор Пойнтинга изменяется по закону

П_A = 5·10^-3cos²(wt– 30°) Bт/м².

Написать выражение для мгновенного значения тока в излучающем проводе.

Ответ:  i = 73sin(wt – 30°) A.

ЗАДАЧА 15.34. У радиостанции мощностью  500 кВт,  работающей на волне 1744 м, передающая антенна расположена вертикально и имеет высоту 150 м.

Считая, что антенна со своим зеркальным изображением может рассматриваться как электрический диполь, определить ток в антенне.

Ответ: I =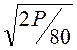·=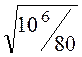·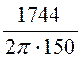= 207A.