Простейшие приёмные антенны. Штыревая антенна радиоприемника (комнатная антенна), страница 9

При анализе принять, что стенки волновода выполнены идеальным проводящим материалом.

Решение

Так как плоскость рамки с током перпендикулярна оси волновода, то векторный электрический потенциал поля имеет только осевую составляющую   =F,   а остальные проекции отсутствуют: F_x = 0,  F_y = 0.

Начало координат декартовой системы координат выберем в одной из вершин прямоугольного волновода в соответствии с рис. 15.28.

Учитывая неограниченную осевую протяжённость волновода, замечаем, что вдоль этого направления отсутствует обратная волна. Тогда решение волнового уравнения относительно векторного электрического потенциала имеет вид:

F= (D₁+ D₂)·(D₃+ D₄)· D₅.

Чтобы электромагнитная волна распространялась вдоль волновода с идеальным диэлектриком при идеальном проводящем материале стенок, должно выполняться условие – коэффициенты разделения k_x, k_y, k_z должны быть действительными числами, а из решения волнового уравнения следует соотношение

k_x² + k_y² + k_z² = k² = w²mm₀ee₀ =, где  v =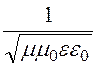= 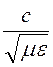– скорость распространения электромагнитной волны в неограниченном по всем направлениям пространстве (такое пространство называют свободным).

Учитывая, что в направлениях осей х и у при отражении волн от стенок идеальной проводящей среды имеют место стоячие волны, получаем следующий вид решения

F= F_z = Dsin(k_xx +y_x)sin(k_yy +y_y).

Напряженность электрического поля

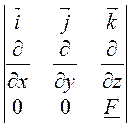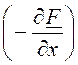= rot==++·0.

Проекции вектора напряженности электрического поля

Е_х == Dk_ysin(k_xx+y_x)соs(k_yy+y_y),

Е_у = -= -Dk_хсоs(k_xx+y_x)sin(k_yy+y_y),

Е_z = 0 – у вектора отсутствует осевая составляющая, а есть только поперечные для волновода составляющие.

Такая волна называется поперечной электрической и обозначается как ТЕ_mn.

При любых  x(0 … а)  и  y= 0   Е_х = 0, откуда

соs(k_yy+y_y) = соs(0 +y_y) = 0,   y_y = ½p.

При любых   x(0 … а)  и  y= b Е_х = 0,  значит

соs(k_yb+ ½p) = 0,   k_yb= np   и коэффициент разделения  k_y=.

При любых   y(0 … b)  и   x= 0    Е_y = 0,   откуда

соs(k_xx+y_x) = соs(0 +y_x) = 0,   y_x = ½p.

При любых    y(0 … b)  и   x= a    Е_y = 0, значит

 соs(k_xa+ ½p) = 0,   k_xa= mp   и коэффициент разделения  k_x=.

Коэффициент разделения

k_z² = k² – k_x² – k_y² = k² – p².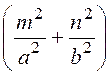

Проекции вектора напряженности электрического поля

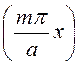Е_х = -Dcossin,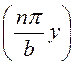

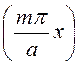Е_у = Dsinсоs,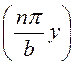

Е_z = 0.

Напряженность магнитного поля согласно второму уравнению Максвелла

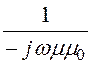=rot,  но  rot= rot rot= grad div– Ñ ².

Из волнового уравнения Ñ ²+ k²= 0  определяем  Ñ ²= -k². Тогда

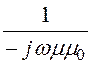=(graddiv+ k²),  a так как   =F,  то

div==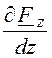 -jk_zF.

Проекции вектора напряженности магнитного поля волновода при наличии ТЕ_mn  волны

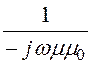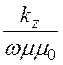
H_х=grad_хdiv== -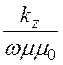E_y,

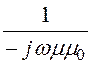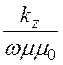
H_y=grad_ydiv==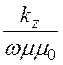E_x,

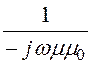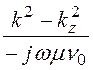H_z=(grad_zdiv+ k ²) =F. 

В приведенных выражениях

k_z ==.

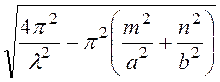Для обеспечения волнового процесса необходимо, чтобы k_z > 0.

Критическая длина волны в волноводе    λ_кр =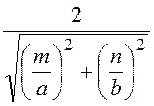, длина волны в волноводе   L ==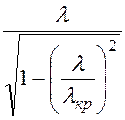> λ.

Заметим, что волны ТЕ_mn  допускают значения m= 0 или n= 0, чего нет для волн ТМ_mn.

Фазовая скорость распространения волны   v_z == Lf=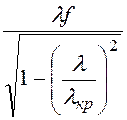, волновое сопротивление ТЕ волны

Z_CTE ===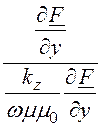=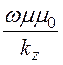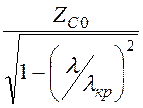, где   Z_{C 0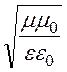}= – волновое сопротивление свободного пространства.

ЗАДАЧА 15.42. Определить, какие типы волн могут распространяться в заполненном воздухом  прямоугольном волноводе размерами    а´b=          = 2,5´5 см² при частоте 7,5∙10⁹ Гц.

Ответ:  ТЕ_0,1; ТЕ_0,2; ТЕ_1,0; ТЕ_1,1; ТМ_1,1.

ЗАДАЧА 15.43. Определить мощность, переносимую электромагнит-ной волной типа ТЕ_0,1в прямоугольном волноводе задачи 15.42, если наибольшее амплитудное значение напряженности электрического поля в волноводе составляет величину   Е_m= 10⁵ В/м.

Ответ:  P = 7,55 кВт.