Простейшие приёмные антенны. Штыревая антенна радиоприемника (комнатная антенна), страница 6

Поток мощности излучения рассчитаем для рамочной антенны по теореме Умова-Пойнтинга   Р + jQ=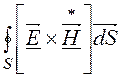,  где элемент сферической поверхности dS = 2pR²sinqdq  (см. задачу 15.32), а   -E_a= П_R  – радиальная составляющая вектора Пойнтинга, совпадающая по направлению с элементом поверхности . Для дальней зоны излучения получаем  Q = 0, активная мощность излучения

Р =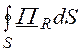=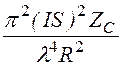·2pR²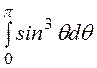=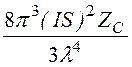, сопротивление излучения чисто активное           r ==.

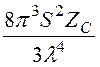В условиях рассматриваемой задачи среда воздушная,  S = pa², Z_C =     = 120p = 377 Ом,  тогда

Р = 320p⁶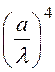I²,    r = 320p⁶.

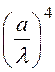Подставив  а = 2∙10^-2 м;   λ = 1,5 м;I= 4 A, получаем

r = 320p⁶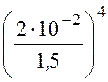= 0,00972 Ом,    Р = 0,156 Bт.

15.3.2. Электромагнитное поле в направляющих средах. Волноводы.

Современная техника сверхвысоких частот, работающая в области дециметровых и сантиметровых волн, применяет вместо обычных передающих линий (проводных или кабельных) волноводы, представляющие собой полую металлическую трубу (прямоугольного, круглого или эллиптического сечения), полость которой служит для передачи электромагнитных волн.

Изучая особенности распространения волн в волноводе, необходимо анализировать решения векторных волновых уравнений общего вида, к которым сводятся уравнения Максвелла, а последние для диэлектрика в комплексной форме представляют систему:

rot= jwee₀;     div = 0;    rot = -jwmm₀;      div = 0.

Разрешая эту систему относительно , получаем векторное волновое уравнение                                                             Ñ ²+ k ²= 0;

разрешая систему относительно , имеем     Ñ ²+ k ²= 0;

решая систему с помощью векторного магнитного потенциала  ,  когда  = rot  или векторного электрического потенциала ,  когда  =rot, получаем аналогичные волновые векторные уравнения:

Ñ ²+ k ²= 0         или         Ñ ²+ k ²= 0.

В этих уравнениях волновое число k = w ==  является действительным числом.

В декартовой системе координат одно векторное волновое уравнение сводится к трем скалярным волновым уравнениям относительно проекций вектора, например,

Ñ ²+ k ²= 0       Þ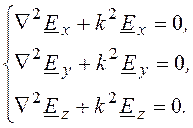   

В произвольной ортогональной системе координат решение в общем виде возможно, только если вектор имеет одно направление – вдоль координаты, для которой метрический коэффициент Ламе    h₁ = 1:

- для цилиндрической – вектор направлен вдоль оси цилиндра;

- для сферической – вектор направлен вдоль радиуса R.

Найдем решение скалярного волнового уравнения в декартовой системе координат для одной из проекций вектора, например, Ñ ²Е_х + k ²Е_х= 0.

После раскрытия  Ñ ²Е_х,  где  Е_х = f(x,y,z),получим уравнение в частных производных

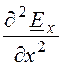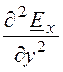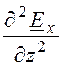+++ k ²Е_х = 0.

Это уравнение можно решить известным способом разделения переменных, если положить  Е_х = X(x)Y(y)Z(z).  После подстановки в вышесто-ящее и сокращения на произведение XYZ получим

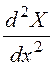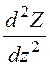+++ k ² = 0.

Поэтому имеем систему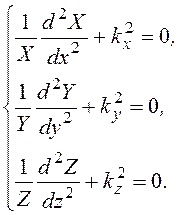   

В этой системе k_x,k_y, k_z– постоянные разделения, удовлетворяющие условию     k_x² + k_y² + k_z² = k² = w²mm₀ee₀, которое можно представить в измененной форме

++= n_x² + n_y² + n_z² = 1.

Для идеального диэлектрика k² положительное число, значит, k– действительное число, n_x, n_y, n_z – также действительные числа. Если три числа n_x, n_y, n_zрассматривать как составляющие единичного вектора , то они являются направляющими косинусами, и через сферические координаты qи a, когда вектор  направлен вдоль координаты  R получаем

n_x = sinqcosa,   n_y = sinqsina,    n_z = cosq.

Таким образом, решения принимают вид      X = D₁+ D₂,

Y = D₃+ D₄,

Z = D₅+ D₆.

ЗАДАЧА 15.37. В прямоугольном волноводе с размерами поперечного сечения а и b(рис. 15.28) и с неограниченной длиной вдоль оси z возбуждаются волны штыревым вибратором, расположенным в начале волновода вдоль оси волновода. Вывести общие выражения для составляющих электромагнитного поля в волноводе.

Определить тип волн.