Простейшие приёмные антенны. Штыревая антенна радиоприемника (комнатная антенна), страница 7

Составить формулы для критической длины волны, фазовой скорости и характеристического сопротивления.

Решение

Для решения задачи воспользуемся декартовой системой координат с началом, расположенным в одной из вершин прямоугольника (рис. 15.28) на стенке, где расположен излучающий вибратор.

Прямолинейный провод вибратора, по которому протекает синусоидальный ток, расположен вдоль оси волновода. Если для расчета состояния волновода воспользоваться векторным магнитным потенциалом, то этот вектор будет в рассматриваемых условиях иметь только одну проекцию, то есть  =А  при  А_х = 0,  А_у = 0,  а векторный потенциал определится решением скалярного волнового уравнения

Ñ ²А+ k ²А= 0, где   k = w==,

v =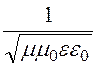 – скорость распространения электромагнитной волны в неограниченном пространстве (свободном пространстве), заполненном идеальным диэлектриком,

λ = v/f  – длина волны в этой среде.

Решение этого волнового уравнения получено выше:

А= (D₁+ D₂)·(D₃+ D₄)· D₅.

Слагаемое  D₆= 0,  оно представляет собой обратную волну, кото-рой в волноводе, неограниченном в размере вдоль оси z, не может быть.

Постоянные разделения удовлетворяют условию

k_x² + k_y² + k_z² = k² = w²mm₀ee₀.

Для идеального диэлектрика k_x,k_y, k_z – действительные числа, представ-ляющие собой коэффициенты фаз прямых и обратных волн, распростра-няющихся вдоль соответствующих осей координат с фазовыми скоростями

v_x =;    v_y =;   v_z =.

Если учесть, что при движении волн в направлениях осей x и y наблюдается полное отражение от стенок идеального проводника, когда амплитуды прямых и обратных волн одинаковы, то

Х= D₁+ D₂= D₇sin(k_xx+y_x),

Y= D₃+ D₄= D₈sin(k_yy +y_y).

Получаем окончательный вид решения волнового уравнения для векторного магнитного потенциала в рассматриваемых условиях работы волновода

A= A_z = Dsin(k_xx +y_x)sin(k_yy +y_y), где     D = D₅D₇D₈.

Напряженность магнитного поля рассчитаем с помощью выражения

= rot.

Из первого уравнения Максвелла

jwee₀= rot= rot(rot) = grad(div) – Ñ ².

Но из волнового уравнение имеем    Ñ ²= -k ²,  тогда

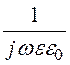=(grad(div) + k ²), причём  k ²=k ²A– слагаемое вектора, имеющее только одну проекцию на ось z.

Рассчитаем проекции вектора , раскрывая  rot:

= rot=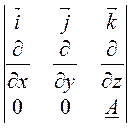,  откуда   Н_х =,   Н_у = -,   Н_z= 0 –

у вектора  отсутствует продольная составляющая, Н_х и Н_y– поперечные составляющие вектора. Такая волна называется поперечной магнитной волной ТМ.

Проекции вектора напряженности электрического поля с учётом     div== -jk_z A

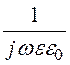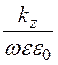
E_х=grad_хdiv= -=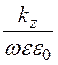Н_y,

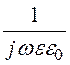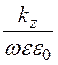
E_y=grad_ydiv= -= -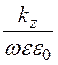Н_x,

E_z=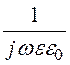(grad_zdiv+ k ²) =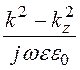A  – электрическое поле в отли-чие от магнитного имеет и продольную составляющую.

Из последнего равенства следует, что E_zи А взаимно связаны. На стенках идеальной проводящей среды волновода  E_z = 0  при  х = 0  и  х = а  и z= 0, а также при  y= 0  и  y= b  и  z= 0, поэтому  А = 0  при тех же условиях.

Эти граничные условия позволяют определить k_x, k_y, y_x, y_yв выражении для векторного магнитного потенциала

A= A_z = Dsin(k_xx +y_x)sin(k_yy +y_y).

Из условия  А = 0  в зависимости от  х  получаем  sin(k_xx + ψ_x) = 0, откуда при  х = 0  и  sinψ_x = 0,ψ_x= 0,  тогда при  х = а  и  sink_xa= 0,  k_xa = mπ  и коэффициент  k_x =, где  m– целое число, начиная сm= 0.

Из условия  А = 0  в зависимости от  y  получаем  sin(k_yy + ψ_y) = 0, откуда при  y= 0  и  sinψ_y = 0,  ψ_y = 0,  тогда при  y= b  и  sink_yb= 0,  k_yb= nπ  и коэффициент  k_y =,  где   n = 0, 1, 2, 3 …

Теперь можем определить

k_z² = k² – k_x² – k_y² =––.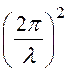

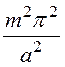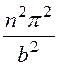Если k_z действительное число, то это число имеет смысл коэффициента фазы волны в волноводе (ωt– k_zz), фазовая скорость этой волны

v_ф ==·= v, где v=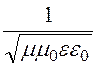 – скорость распространения волны в диэлектрике неограни-ченных размеров.

Так как  k/k_z > 1,  то   v_ф  > v.

Длина волны в волноводе     L ==·= λ> λ, где   λ – длина волны в свободном пространстве.