Линейные цепи постоянного тока. Основные теоретические положения

Точка электрической цепи называ-ется узлом, если в ней соединены три или большее число ветвей (рис. 1.5, узел А).

Контур электрической цепи представляет собой замкнутый путь по ветвям электрической цепи, причём каждая ветвь и каждый узел на пути встречаются лишь однажды.

Для составления уравнений по законам Кирхгофа необходимо задаться положительными направлениями токов в каждой ветви.

Согласно первому закону Кирхгофа алгебраическая сумма токов в узле равна нулю. Математически: 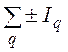  = 0.     Здесь токи, направленные к узлу, берутся со знаком «минус», а токи, направленные от узла – с «плюсом».

Согласно второму закону Кирхгофа в любом замкнутом контуре электрической цепи алгебраическая сумма падений напряжений на отдельных участках равна алгебраической сумме действующих в этом же контуре ЭДС: 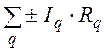=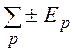. Направление обхода контура выбирается произвольно, ЭДС и напряжения, направления которых совпадают с обходом контура, учитываются в уравнении со знаком «плюс», а направленные против обхода – со знаком «минус». При составлении уравнений должно соблюдаться правило, чтобы в каждом следующем контуре была хотя бы одна ветвь, не вошедшая в предыдущие контуры. Такие контуры называют независимыми. Второй закон Кирхгофа нельзя применять к контурам, содержащим источники тока.

Универсальной проверкой расчёта токов является составление баланса мощностей (БМ), который является следствием из закона сохранения энергии и гласит, что мощность источников равна мощности потребителей. По поводу составления БМ см. задачу 1.6.

1.2. РАСЧЁТ ЦЕПЕЙ ПО ЗАКОНАМ ОМА И КИРХГОФА

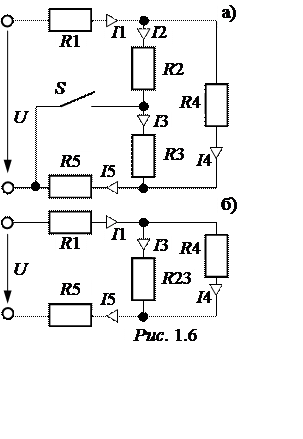Задача 1.1. В цепи рис. 1.6,а определить токи при двух положениях ключа  S,  если  R1 = 4 Ом,   R2 = 1 Ом,    R3 = 2 Ом,  R4 = 6 Ом,   R5 = 6 Ом,   U = 36 В.

Решение

1. Укажем положительные направле-ния токов (рис. 1.6,а). Выполним расчёт цепи при разомкнутом ключе  S. Резисторы R2 и R3 соединены последовательно, заменяем их одним эквивалентным:

R23 = R2 + R3 = 1 + 2 = 3 Ом.

Получаем схему рис. 1.6,б.

Параллельно соединённые резисторы R23 и R4 заменяем сопротивлением

R234 = R23×R4/(R23 + R4) = 3×6/(3+6) = 2 Ом.

Получаем цепь с последовательным соединением резисторов   R1-R234-R5.

Входное сопротивление полученной цепи:

Rвх = R1 + R234 + R5 = 4 + 2 + 6 = 12 Ом.

Входной ток по закону Ома

I1 = I5 = U/Rвх = 36/12 = 3 А.

Остальные токи определяем по правилу разброса тока в параллельные ветви:

I2 = I3 = I1×R4/(R23+R4) = 3×6/9 = 2 А;

I4 = I1×R23/(R23+R4) = 3×3/9 = 1 А.

2. Выполним расчёт цепи при замкнутом ключе S (рис. 1.7,а).

В связи с неочевидностью вида соединения сопротивлений пронумеруем точки,  имеющие разные потенциалы (см. рис. 1.7,а), и перечертим  схему  в  более наглядном виде (рис. 1.7,б). Два узла обозначены цифрой «3», так как они соединены перемычкой и, следовательно, имеют одинаковый потенциал. В этой цепи резисторы R3 и R5 соединены параллельно, поэтому

R35 = R3×R5/(R3 + R5) = 2×6/(2 + 6) = 1,5 Ом.

Полученное сопротивление R35 соединено последовательно с R4:

R354 = R35 + R4 = 1,5 + 6 = 7,5 Ом.

Далее имеем параллельное соединение R354||R2:

R3542 = R354×R2/(R354 + R2) = 7,5×1/(7,5 + 1) = 0,882 Ом.

Входное сопротивление цепи:

Rвх = R1 + R3542 = 4 + 0,882 = 4,882 Ом.

Теперь вычисляем токи:

I1 = U/Rвх = 36/4,882 = 7,374 А;

I2 = I1×R354/(R354 + R2) = 7,374×7,5/8,5 = 6,506 А;

I4 = I1×R2/(R354 + R2) = 7,374×1/8,5 = 0,868 А;

I5 =I4×R3/(R3 + R5)= 0,868×2/(2 + 6) = 0,217 А;

I3 = I5 – I4 = 0,217 – 0,868 = -0,651 А.

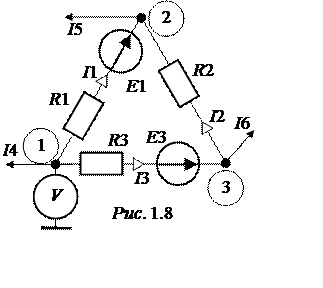
Задача 1.2. Потенциалы узлов участка цепи рис. 1.8 измерены вольтметром Vи равны:  j1 = -15 В,  j2 = 52 В,  j3 = 64 В.

Используя закон Ома и первый закон Кирхгофа определить все показанные на рисунке токи, если  R1 = 5 Ом,  R2 = 10 Ом,  R3 = 12 Ом,  Е1 = 80 В,  Е3 = 70 В.

Решение

1.  В соответствии с законом Ома в обобщённой форме вычисляем:

I1 = (j1 – j2 + Е1)/R1 = (-15 – 52 + 80)/5 = 2,6 А;

I2 = (j3 – j2)/R2 = (64 – 52)/10 = 1,2 А;

I3 = (j1 – j3 + Е3)/R3 = (-15 – 64 + 70)/12 = -0,75 А.

2.  По первому закону Кирхгофа находим остальные токи:

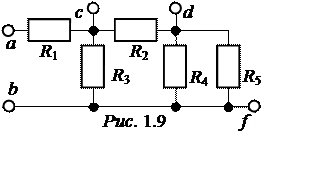I4 = -(I1+ I3) = -(2,6 – 0,75) = -1,85 А;

I5 = I1+ I2 = 2,6 + 1,2 = 3,8 А;

I6 = I3 – I2 = -0,75 – 1,2 = -1,95 А.

ЗАДАЧА 1.3.   Для   схемы   цепи рис. 1.9 найти эквивалентные сопротивле-ния между зажимами  a и b,  c и  d,  d  и  f,  если   R₁ = 6 Ом,  R₂ = 5 Ом,  R₃ = 15 Ом,   R₄ = 30 Ом,   R₅ = 6 Ом.

Ответы:        R_df == 4 Ом,

R_ab =  R₁ +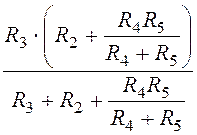= 12 Ом,       R_cd =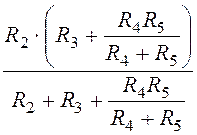= 4 Ом.

ЗАДАЧА 1.4. Определить сопротивление цепи между точками a и b при разомкнутом и замкнутом контакте S (рис. 1.10) если

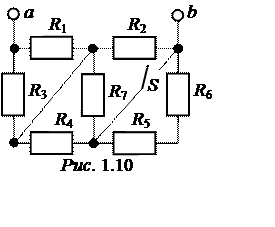R₁ = R₂ = R₃ = R₄ = R₅ = R₆ = R₇ = 10 Ом.

Ответ: при разомкнутом контакте 12,1 Ом,  при замкнутом – 8,33 Ом.

ЗАДАЧА 1.5. Определить сопротивление каждой из цепей рис. 1.11 между зажимами 1-1¢ при холостом ходе (точки 2 и 2¢ разомкнуты) и при коротком замыкании (точки 2 и 2¢ закорочены). Сопротивления в омах даны на схеме.

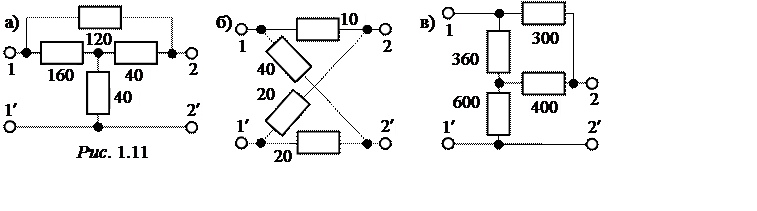Ответы: а) R_1Х = 120 Ом,  R_1К = 72 Ом;   б) R_1Х = 20 Ом,  R_1К = 18 Ом;

в) R_1Х = 838 Ом,  R_1К = 200 Ом.

ЗАДАЧА 1.6. Внешняя характеристика генератора постоянного тока, снятая экспериментально по схеме рис. 1.12,а, приведена на рис. 1.12,б. Начальный участок внешней характеристики достаточно точно описывается уравнением прямой линии  U = 110 – 0,25×i,  где  U[B],  I[A].

Номинальный ток генератора  i_НОМ = 40 А,  настройка максимальной токовой защиты  i_max = 60 А,  реальный ток короткого замыкания  i_КЗ = 200 А.

Построить схемы замещения генератора и найти их параметры