P:=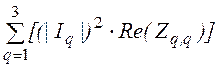 +
+ 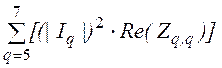 + (|I4 + J4|)2×Re(Z4,4)
+ (|I4 + J4|)2×Re(Z4,4)
P= 3.506×103
Q:=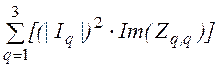 +
+ 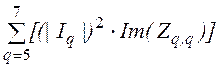 + (|I4 + J4|)2×Im(Z4,4)+
+ (|I4 + J4|)2×Im(Z4,4)+
+ 2×Im(I1×![]() ×j×Im(Z1,2)) + 2×Im(I6×
×j×Im(Z1,2)) + 2×Im(I6×![]() ×j×Im(Z6,7))
×j×Im(Z6,7))
Q = –1.762i×103
4. ТРЁХФАЗНЫЕ ЦЕПИ
4.1. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Теория трёхфазных систем начинается с введения понятий: симметричные системы ЭДС, напряжений, токов; несимметричные системы ЭДС, напряжений, токов.
Краткий перечень названий ЭДС, напряжений, токов следующий:
- фазные ЭДС eA, eB, eC соответствующих фаз генератора AX, BY, CZ;
- фазные токи IAX, IBY, ICZ ;
- фазные напряжения UAX, UBY, UCZ ;
- линейные напряжения UAB, UBC, UCA ;
- линейные токи IA, IB, IC ;
- ток нейтрали (нулевого провода) IN ;
- напряжение смещения нейтрали UN или ![]() (между нулевыми точками
генератора и приёмника).
(между нулевыми точками
генератора и приёмника).
Соответственно, различают активные, реактивные, полные мощности фаз PA, PB, PC, QA, QB, QC, SA, SB, SC, а также активную P, реактивную Q и полную S мощности трёхфазных приёмников (или генератора), причём
P
= PA + PB + PC , Вт; Q = QA + QB + QC , вар; S=![]() , ВА.
, ВА.
Трёхфазные цепи со статической нагрузкой, то есть не содержащие электродвигателей, трансформаторов и других активных элементов рассчитываются, как правило, комплексным методом. Их расчёт обычно сопровождается построением векторных или топографических диаграмм, которые предостерегают от возможных ошибок аналитических расчётов, делают все соотношения более наглядными.
Если в трёхфазной системе имеются устройства, сопротивления фаз которых зависят от системы токов (трёхфазные трёхстержневые трансформаторы, асинхронные или синхронные электродвигатели или генераторы, или хотя бы одно из таких устройств, мощность которого соизмерима с мощностью всей трёхфазной системы), то для расчёта несимметричного режима таких трёхфазных цепей применяют специальный метод расчёта – метод симметричных составляющих, который по сути своей является разновидностью метода наложения.
4.2. РАСЧЁТ СИММЕТРИЧНЫХ ТРЁХФАЗНЫХ ЦЕПЕЙ
Расчёт симметричных трёхфазных цепей сводится по сути к расчёту одной фазы по однолинейной эквивалентной схеме. В двух других фазах будут такие же по величине токи и напряжения, как в первой, но сдвинуты по фазе относительно них на угол 120°.
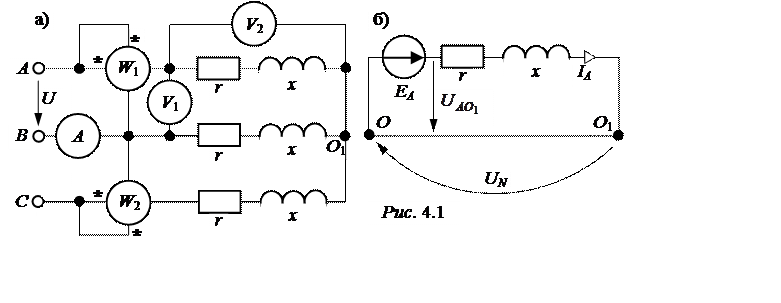
ЗАДАЧА
4.1. К симметричной трёхфазной цепи с напряжением U
= 380 B подключен симметричный приёмник, фазы которого
соединены в «звезду» (рис. 4.1,а), сопротивления фаз r
= 12 Ом, х = 16 Ом.
Найти показания приборов, построить векторную диаграмму цепи.
Решение
Когда говорят о напряжении трёхфазной цепи, подразумевают линей-ное напряжение сети (по умолчанию). Если задаётся фазное напряжение, то это подчёркивается специально.
В условиях нашей задачи напряжение сети U = 380 B, причём по условию симметрии:UАВ = UВС = UСА = U = 380 B.
Фазные напряжения меньше линейных в ![]() раз:
раз:
UА = UВ = UС = U/![]() = 380/
= 380/![]() = 220 B.
= 220 B.
Предположим, что фазы генератора соединены в звезду, тогда фазные ЭДС генератора ЕА = ЕВ = ЕС = UФ = 220 B.
В симметричной системе Y-Y узловое напряжение UN = 0и расчёт состояния цепи можно вести по схеме замещения для одной фазы (рис. 4.1,б).
Примем ЕА = 220 B, ток в схеме замещения
IА =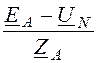 =
=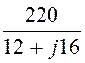 = 11×e –j53,13° A, причём
фазное напряжение приёмника
= 11×e –j53,13° A, причём
фазное напряжение приёмника ![]() = ЕА – UN = ЕА
= UА.
= ЕА – UN = ЕА
= UА.
Результаты расчёта режима работы остальных фаз (В и
С) запишем на основании понятия о симметричной трёхфазной системе
прямого порядка следования фаз ЕВ = ![]() = UB = ЕА×e –j120° = 220×e –j120° B;
= UB = ЕА×e –j120° = 220×e –j120° B;
ЕC = ![]() = UC = ЕА×e j120° = 220×e j120° B;
= UC = ЕА×e j120° = 220×e j120° B;
аналогично для токов IВ = IА×e –j120° = 11×e –j173,13° A;
IC = IА×e j120° = 11×e j66,87° A.
Векторная диаграмма цепи приведена на рис. 4.2, для которой потенциал нулевой точки генератора, обмотки которого соединены в «звезду», j O = 0(рис. 4.1,б).
j A = ЕА = 220 B; j B = 220×e –j120° B; j C = 220×e j120° B; ![]() = j O + UN = 0;
= j O + UN = 0;
UAO = j A – j O = ЕА = ![]() = j A –
= j A – ![]() = UA
= 220 B; аналогично UB = j B – j O = 220×e –j120° B; UC = j C – j O = 220×e j120° B;
= UA
= 220 B; аналогично UB = j B – j O = 220×e –j120° B; UC = j C – j O = 220×e j120° B;
 а токи фаз ориентированы относительно своих фазных
напряжений (сдвину-ты на угол j = arctg
а токи фаз ориентированы относительно своих фазных
напряжений (сдвину-ты на угол j = arctg![]() = arctg
= arctg![]() =
53,13°).
=
53,13°).
Линейные напряжения:
UAВ = j A - j В =UA×![]() ×e j30°=
×e j30°=
= 380×e j30° B;
UВС = UAВ×e –j120° = 380×e –j90° B;
UСA = UAВ×e j120° = 380×e j150° B.
Напряжения и токи кату-шек ваттметров:
UW1 = UAВ = 380×e j30° B;
IW1 = IA = 11×e –j53,13° A;
UW2 = -UВC = 380×e j90° B;
IW2 = IC = 11×e j66,87° A.
Показания приборов:
- амперметр A измеряет линейный ток IB и его показание IB = 11 A;
- вольтметр V1 измеряет линейное напряжение UAВ = 380 B;
- вольтметр V2 измеряет фазное напряжение приёмника
UA = 220 B;
- показания ваттметров:
PW1 = Re[UW1×![]() ] = Re[UAB×
] = Re[UAB×![]() ] = UAВ×IA×cos(j + 30°)=
] = UAВ×IA×cos(j + 30°)=
= 380×11×cos(53,13°+30°)= 500 Вт;
PW2 = Re[UW2×![]() ] = Re[UСВ×
] = Re[UСВ×![]() ] = UСВ×IС ×cos(j– 30°)=
] = UСВ×IС ×cos(j– 30°)=
= 380×11×cos(53,13° – 30°)= 3846 Вт.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.