Трёхфазные цепи. Основные теоретические положения, страница 7

r_A =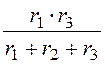==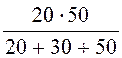 10 Ом;

r_В =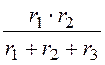==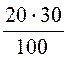 6 Ом;   r_С =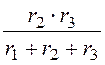==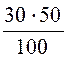 15 Ом.

Примем Е_А = 73,3 B, тогда  Е_В = 73,3×e ^–j120°B, Е_С = 73,3×e ^j120°B.

Узловое напряжение

U_N ===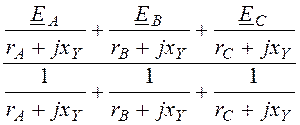

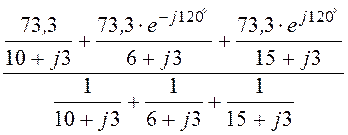= -17,05×e ^j61,99°= -8 – j15,05 B.

Линейные токи

I_А =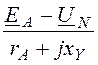==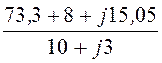 7,87 – j0,857 A;

I_B =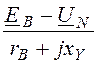==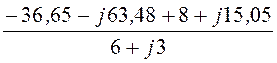 -7,047 – j4,545 A;

I_C =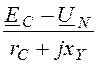==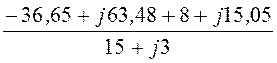 -0,829 + j5,397 A.

Линейное напряжение на нагрузке

U_AB = I_А×r_A – I_B×r_B = (7,87 – j0,857)×10 – (-7,047 – j4,545)×6 =

= 121 + j18,7 = 122,4×e ^j8,79°B.

Фазные токи осветительной нагрузки (рис. 4.21)

I_ab =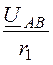==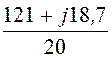 6,05 + j0,935 = 6,122×e ^j8,79° A;

I_ca = I_ab – I_А = 6,05 + j0,935 – 7,87 + j0,857 = -1,82 + j1,792 = 2,554×e ^j135,44° A;

I_bc = I_ab + I_B = 6,05 + j0,935 – 7,047 – j4,545 = -0,997 – j3,61 = 3,745×e ^-j105,44° A.

Линейные напряжения

U_BC = I_bc ×r₂ = 112,4 B,    U_CA = I_ca ×r₃ = 127,7 B.   

Активная мощность осветительной нагрузки и генератора

P= P_АB + P_BC + P_CA = I_ab²×r₁ + I_bc²×r₂ + I_ca²×r₃ =

= 6,122²×10 + 3,745²×30 + 2,554²×50 = 1122 Вт = 1,122 кВт.

Фазные токи источника питания (см. задачу 4.17)

i_АХ=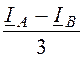= 4,972 + j1,229 = 5,122×e ^j13,88° A;

i_ВY=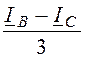= -2,073 – j3,314 = -3,91×e ^j57,97° A;

i_СZ=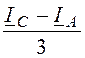= -2,9 + j2,085 = -3,572×e ^-j35,71° A.  

Реактивная мощность генератора (и всей цепи)

Q= Q_АX + Q_BY + Q_CZ = I_АX²×x + I_BY²×x + I_CZ²×x =

= 9×(5,122² + 3,91² + 3,572²) = 488,5 вар = 0,4885 квар.

Полная мощность источника питания

S=== 1,224 кВA.

Коэффициент мощности источника питания  cosj ===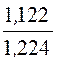 0,917.

ЗАДАЧА 4.19. Трёхфазная цепь (рис. 4.23) подключена к симметрич-ному генератору с напряжением U= 660 B. Параметры цепи

r = wL== 10 Ом, r₁ = wL₁= 5 Ом.

Рассчитать линейные и фазные токи всех участков цепи.

Решение

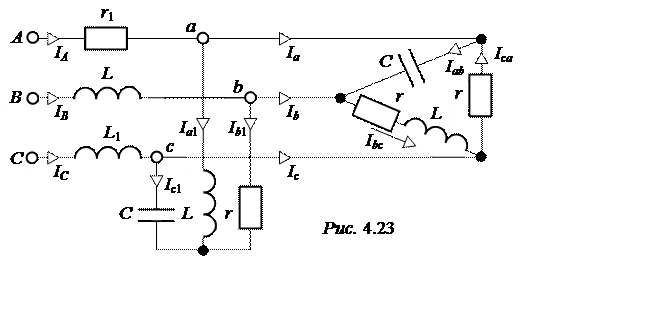Упростим схему, используя метод эквивалентных преобразований.

Сначала несимметричную звезду без нулевого провода заменим эквивалентным треугольником сопротивлений:

Z_ab1 = jwL + r +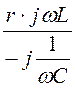= j10 + 10 +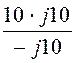= j10 Ом,

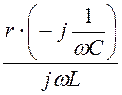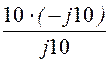Z_bc1 = r – j+= 10 – j10 + = -j10 Ом,

Z_ca1 = jwL – j+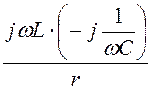= j10 – j10 + 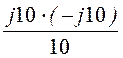= j10 Ом.

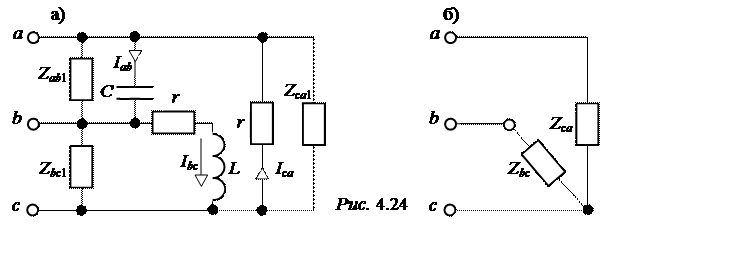
Теперь два треугольника сопротивлений оказываются включенными параллельно (рис. 4.24,а).

Эти два треугольника можно заменить одним с сопротивлениями фаз

Z_ab =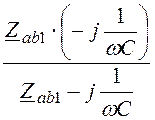==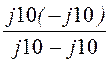 ¥,   следовательно,   в этом параллельном контуре без потерь наблюдается резонанс токов и входное сопротивление этого контура бесконечно большое (разрыв цепи по отношению к остальной схеме);

Z_bс =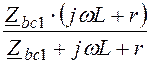==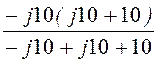 10 – j10 Ом;

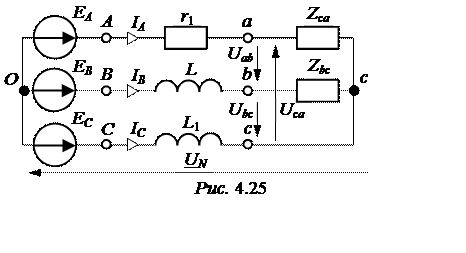Z_са =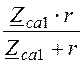==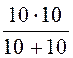 5 Ом.

В результате получаем схему замещения нагрузки, подключенной на зажимы  a-b-с, представленную на рис. 4.24,б.

Представим, что обмотки симметричного трёхфазного источника ЭДС соединены в звезду с ЭДС   Е === 380 В = Е_А.

Получаем преобразованную схему рис. 4.25. Для этой схемы

U_N ===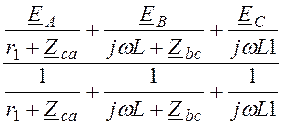

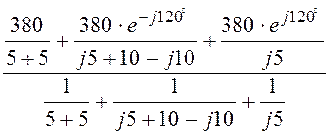= 200 + j225 B.

Линейные токи генератора

I_А =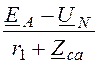==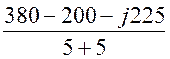 18 – j22,5 A;

I_B =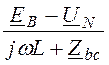==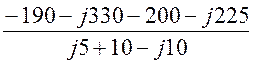 -39 – j55,5 A;

I_C =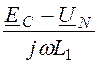==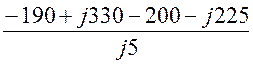 21 + j78 A.

Линейные напряжения на зажимах приёмников на основании схемы рис. 4.25:

U_ab = I_А×Z_ca – I_B×Z_bc = (18 – j22,5)×5 – (-39 – j55,5)×(10 – j10) = 1035 + j52,5 B;

U_bc = I_B×Z_bc = (-39 – j55,5)×(10 – j10) = -945 – j165 B;

U_ca = -I_A×Z_ca = -(18 – j22,5)×5 = -90 + j112,5 B.

Возвращаемся к исходной схеме рис. 4.23 и находим фазные токи треугольника            I_ab =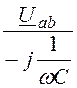==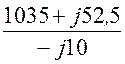 -5,25 + j103,5 A;

I_bc =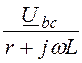==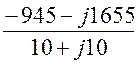 -55,5 + j39 A;

I_ca ===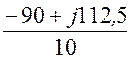 -9 + j11,25 A.

Линейные токи треугольника      I_a = I_ab – I_ca = 3,75 + j92,25 A;

I_b = I_bc – I_ab = -50,25 – j64,5 A;

I_c = I_ca – I_bc = 46,5 – j27,75 A.

Токи приёмника, соединённого в звезду, рассчитаем по I закону Кирхгофа:                                                 I_a1 = I_A – I_a = 14,25 – j114,75 A;

I_b1 = I_B – I_b = 11,25 + j9 A;

I_c1 = I_C – I_c = -56,5 + j105,75 A.

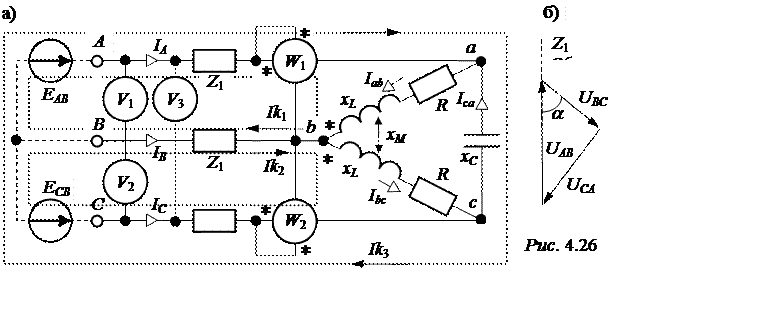
ЗАДАЧА 4.20. В схеме рис. 4.26,а определить токи во всех ветвях, если показания вольтметров: U₁ = 220 В,  U₂ =127 В,  U₃ =191,3 В, а   Z₁ = 3 + j4 Ом,  R = 20 Ом,   x_L = 30 Ом,   x_M = 25 Ом,   x_C = 40 Ом.     Рассчитать показания ваттметров и сравнить их с тепловыми потерями в треугольнике нагрузки.

Решение

Дано:  U1 := 220    U2 := 127   U3 := 191,3      ORIGIN := 1   j :=