Трёхфазные цепи. Основные теоретические положения, страница 2

Обращаем внимание на сумму показаний двух ваттметров:

P_W1 + P_W2 = U×I×cos(j + 30°) + U×I×cos(j– 30°) =

= U×I×cos30°×cosj– U×I×sin30°×sinj + U×I×cos30°×cosj + U×I×sin30°×sinj =

= 2×U×I×cos30°×cosj = 2×U×I××cosj =×U×I×cosj = P  – активная мощностьсимметричного приёмника. В нашем примере

×U×I×cosj =×380×11×cos(53,13°) = 4346 = 500 + 3846 Вт.

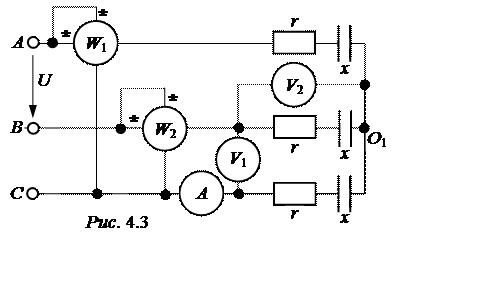ЗАДАЧА 4.2.    Рассчитать симметричный режим соединения в звезду    (рис. 4.3), если    r = 40 Ом,     х = 80 Ом, напряжение сети   U = 380 B.

Построить   векторную   диаграмму цепи.

Ответы: I_С = 2,46 А;

U_В = 220 B;      U_ВС = 380 B;

P_W1 = -56 Вт;  P_W2 = 780 Вт;

P_W1 + P_W2 = 3×I²×r = 726 Вт.

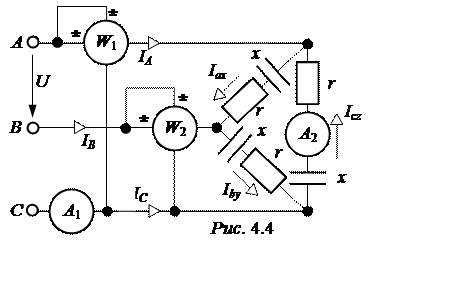
 ЗАДАЧА 4.3. Фазы при-ёмника задачи 4.2 пересоеди-нены в треугольник (рис. 4.4). Рассчитать режим работы схе-мы. Найти отношение линей-ных токов  I_D  схемы рис. 4.4 к линейным токам  I_Y  рис. 4.3.

Решение

При соединении приём-ника в треугольник его линей-ные напряжения равны фазным напряжениям. Примем U_AВ = U = 380 B. Тогда

U_AХ =  U_AВ = 380 B;        U_ВY =380×e ^–j120°B;          U_СZ = 380×e ^j120°B.

Фазные токи рассчитаем по закону Ома:

I_ax =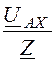==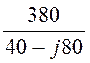 4,25×e ^j63,44° A;

I_by =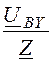= I_ax×e ^–j120° = 4,25×e ^–j56,56° A;

I_cz =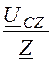= I_ax×e ^j120° = 4,25×e ^j183,44° A.

Линейные токи находим по первому закону Кирхгофа:

I_A = I_ax – I_cz =I_ax×e ^-j30° = 7,36×e ^j33,44° A;

I_B = I_by – I_ax =I_by×e ^-j30° = I_A ×e ^–j120° = 7,36×e ^–j86,56° A;

I_C = I_cz – I_by =I_cz×e ^-j30° = I_A ×e ^j120° = 7,36×e ^j153,44° A.

Векторную диаграмму токов и напряжений соединения в треугольник строим так, чтобы удобно было показывать соотношение между линейными и фазными токами. Для этого исходящими из одной точки построим векторы фазных напряжений треугольника (рис. 4.5,а), относительно них ориентируем фазные токи треугольника, линейные токи находим в соответствии с первым законом Кирхгофа. На основании соотношений между токами, представленными на векторной диаграмме, можно наглядно получить записанные выше соотношения для расчёта линейных токов.

Заметим, что при построении векторной диаграммы треугольника можно пользоваться и традиционным способом построения топографической диаграммы комплексных потенциалов (рис. 4.2), ориентируя фазные токи треугольника относительно линейных напряжений сети, равных фазным напряжениям треугольника, как это показано на рис. 4.5,б. Однако при таком способе построения линейных токов необходимо переносить фазные токи с обратным направлением.

На основании расчётов запишем показания амперметров:

- линейный ток  I_A = 7,36 Aизмеряет амперметр А₁;

- фазный ток треугольника измеряет амперметр А₂, его показание I_cz = 4,25 A.

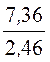При   соединении   тех   же  сопротивлений   в  звезду  линейные  токи  I_Y = 2,46 A (задача 4.2). Таким образом, при переключении фаз приёмника со звезды на треугольник при прежнем напряжении сети линейный ток увеличивается в   == 3 раза.

Показания ваттметров в схеме рис. 4.4:

P_W1 = Re[U_AС ×] = Re[-380×e ^j120°×7,36×e ^–j33,44°] = -168 Вт;

P_W2 = Re[U_ВС ×] = Re[380×e ^-j120°×7,36×e ^j86,56°]= 2334 Вт.

Сумма показаний двух ваттметров  P_W1 + P_W2 = 2167 Вт  по-прежнему равна активной мощности трёхфазного приёмника

P = 3×I_Ф×r_Ф = 3×4,25²×40 = 2167 Вт.

ЗАДАЧА 4.4. Найти показания приборов в схеме рис. 4.6,а, если

r = 76 Ом,   x = 44 Ом,  U = 380 B.

Решение

Представим схему замещения рассматриваемой симметричной трёх-фазной цепи для основной фазы (А) (рис. 4.6,б) и определим её параметры:

- фазное напряжение источника питания    U_A === 220 B,

- сопротивление фазы эквивалентной треугольнику звезды    r_Y == Ом.

Дальнейший расчёт выполним в комплексной форме, приняв U_A=220 B:

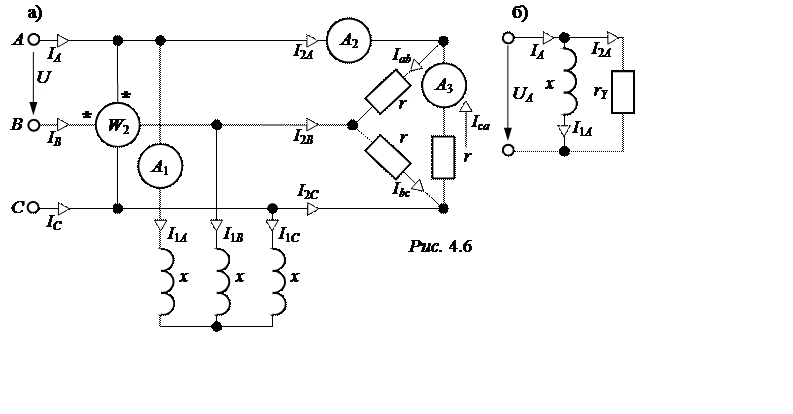
- фазный ток 1-го приёмника, соединенного в звезду     I_1A === -j5 A;

- линейный ток треугольника       I_2A ===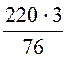= 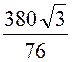5 A.

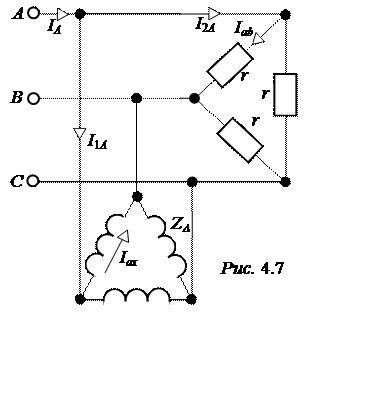Схема замещения рис. 4.6,б не позволяет рассчитать фазный ток симметричного треугольника, который меньше линейного в  раз и не совпадает с ним по фазе (см. решение задачи 4.3):