Z1 := 3 + j4 R := 20 xL := 30 xM := 25 xC := 40
Используя теорему косинусов, с помощью качественно построенной векторной диаграммы линейных напряжений (рис 4.26,б) определим их комплексы, совместив с вещественной осью UAB:
a:= acos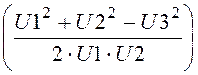
![]() = 60.008
= 60.008
UAB := U1 UBC := U2×e j×(a - p) UCA := – UAB – UBC
Проверка: |UCA| = 191.3
Припишем систему линейных напряжений двум ЭДС (рис. 4.26,а) EAB= UABи ECB= -UBC, а расчёт токов в этой схеме произведём методом контурных токов. Определим собственные и взаимные комплексные сопротивления контуров
Z11 := 2×Z1 + R+ j×xL Z22 := 2×Z1 + R+ j×xLZ33 := 2×Z1 – j×xC
Z12 := – Z1 – j×xMZ13 := Z1 Z23 := Z13
Матрицы контурных сопротивлений, ЭДС и токов
Zk :=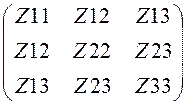 Ek :=
Ek :=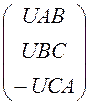 Ik := Zk -1×Ek Ik =
Ik := Zk -1×Ek Ik = 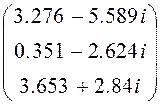
Токи в ветвях IA := Ik1 + Ik3 IB := Ik2 – Ik1 IC := – Ik2 – Ik3
Iab := Ik1 Ibc := Ik2 Icz := – Ik3
Показания ваттметров
Uab := UAB + Z1×(IB – IA) Ucb := – UBC + Z1×(IB – IC)
P1 := Re(Uab×![]() ) P2
:= Re(Ucb×
) P2
:= Re(Ucb×![]() )
)
Тепловые потери в треугольнике Pt := R×(|Iab|2 + |Ibc|2)
Ответы IA = 6.929 – 2.749i Iab = 3.276 – 5.589i
IB = -2.925 + 2.965i Ibc = 0.351 – 2.624i
IC = -4.004 – 0.216i Ica = -3.653 – 2.84i
P1 = 1.222´103 P2 = -242.909 P1 + P2 = 979.437 Pt = 979.437
Сумма показаний ваттметров равна тепловым потерям в треугольнике нагрузки. Таким образом, ваттметры, включенные по представленной схеме, измеряют активную мощность нагрузки.
4.4. ОСОБЫЕ СЛУЧАИ НЕСИММЕТРИИ В ТРЁХФАЗНЫХ ЦЕПЯХ
Рассматриваются простейшие трёх- и четырёхпроводные цепи генератор-приёмник с соединением фаз приёмника и генератора в звезду и треугольник. К особым случаям несимметрии относят обрывы проводов и фаз, короткие замыкания фаз, если исходная схема работает в симметричном режиме. В этом случае цепь перестаёт быть симметричной, однако имеет место ряд особенностей, облегчающих расчёт.
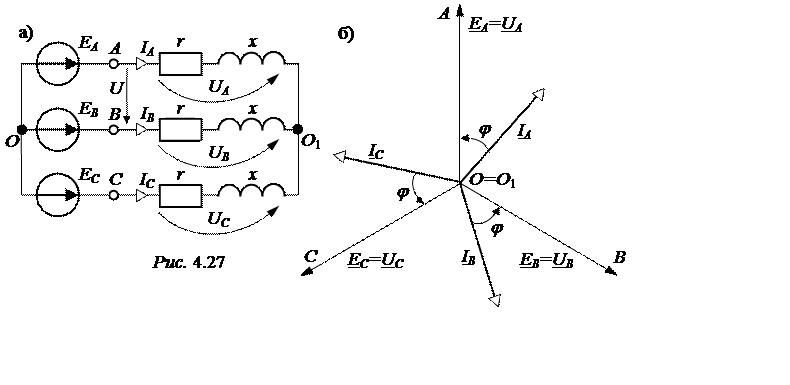
ЗАДАЧА 4.21. Для симметричной трёхфазной системы «звезда-звезда без нулевого повода» (рис. 4.27,а) рассчитать режимы работы следующих случаев: - симметричный режим;
- обрыв линейного провода А;
- короткое замыкание фазы А.
Параметры схемы: U = 380 В, r = x = 20 Ом.
Решение
На рис. 4.27,б приведена векторная диаграмма симметричного режима системы Y-Y. При этом напряжение между нулевыми точками симметричной системы UN= 0.
Фазные ЭДС генератора и фазные напряжения приёмника
EA = UA =![]() =
=![]() = 220 B; EB = UB = 220×e
–j120° B;
EC = UC = 220×e j120° B;
= 220 B; EB = UB = 220×e
–j120° B;
EC = UC = 220×e j120° B;
а также токи IA =![]() =
=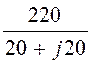 = 7,78×e –j45° А;
= 7,78×e –j45° А;
IВ = IA×e –j120° = 7,78×e –j165° А; IС = IA×e j120° = 7,78×e j75° А
образуют симметричные системы векторов.
При обрыве линейного провода А последовательно с сопротивлением этой фазы Z= r+ jx = 20 + j20 Ом можно считать включенным дополнительное сопротивление обрыва Zобр = ¥, при этом сопротивление ветви А становится равным ZА = Zобр + Z = ¥. Узловое напряжение (его называют напряжением смещения нейтрали)
UN=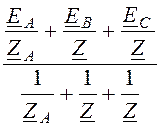 =
=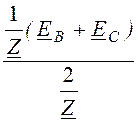 = -
= -![]() = -
= -![]() = -110 B.
= -110 B.
При подсчёте учтено, что при обрыве провода А проводимость
![]() =
=![]() = 0, отношение
= 0, отношение ![]() =
=![]() = 0, и в симметричной
системе
= 0, и в симметричной
системе
EA + EB + EC º 0, откуда EB + EC = -EA.
Напряжение на сопротивлении ZА UA = EA – UN = 1,5×EA = 330 B
является напряжением между точками обрыва провода А,
а ток оборванного провода IA =![]() =
=![]() =
0.
=
0.
Напряжения и токи неповреждённых фаз
UB = EB – UN = 220×e –j120° +110 = -j190 B;
IB =![]() =
=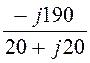 = 6,72×e –j135° A;
= 6,72×e –j135° A;
UC = EC – UN = 220×e j120° +110 = j190 B;
IC =![]() =
=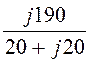 = 6,72×e j45° A.
= 6,72×e j45° A.
Заметим, что при обрыве линейного провода трёхфазная
цепь превращается в однофазную, поэтому токи неповреждённых фаз можно найти и
более простым способом: IB = -IC =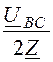 =
=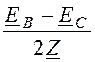 .
.
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.