Трёхфазные цепи. Основные теоретические положения, страница 6

Найти показания ваттметров, сравнить их с активной мощностью несимметричного трёхфазного приёмника.

Решение

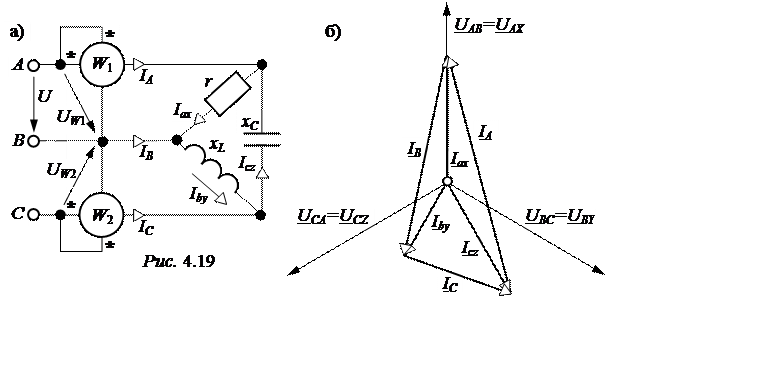
При подключении треугольника сопротивлений к трёхфазному генератору линейные напряжения генератора равны фазным напряжениям нагрузки. Примем  U_AB = 380 B= U_AX,  тогда

U_BY = U_BC = 380×e ^-j120°B,     U_CZ = U_СA = 380×e ^j120°B.

По закону Ома находим фазные токи треугольника

I_ax =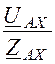== 3,8 А;    I_by =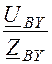==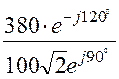 1,9×e ^–j210° А;

I_cz =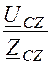==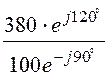 3,8×e ^j210° А.     

Линейные токи находим по I закону Кирхгофа

I_A = I_ax – I_cz = 3,8 – 3,8×e ^j210° = 3,8 + 3,3 + j1,9 = 7,1 + j1,9 = 7,35×e ^j15° А;

I_В = I_by – I_ax = -2,3 + j1,34 – 3,8 = -6,13 + j1,34 = -6,28×e ^–j12,33° А;

I_С = I_cz – I_by = -3,3 – j1,9 + 2,33 – j1,34 = -0,97 – j3,24 = -3,38×e ^j73,33° А.    

Векторная  диаграмма  треугольника  сопротивлений  приведена  на рис. 4.19,б.

Показания ваттметров

P_W1 = Re[U_AB× ] = Re[380×(7,1 – j1,9)] = 2698 Вт,

P_W2 = Re[U_СB× ] = Re[-380×e ^–j120°×(-3,38×e ^-j73,33°)] = -1250 Вт.

Активная мощность несимметричного приёмника

Р = Р_АХ + Р_ВY + Р_СZ = I_ах²×r = 3,8²×100 = 1444 Вт.

Сумма показаний двух ваттметров схемы рис. 4.19,а

P_W1 + P_W2 = 2698 – 1250 = 1448 Вт = Р.

Таким образом, приведенная схема включения двух ваттметров есть схема измерения активной мощности в трёхфазной трёхпроводной цепи, а отличие в четвёртом знаке результатов есть следствие округления чисел.

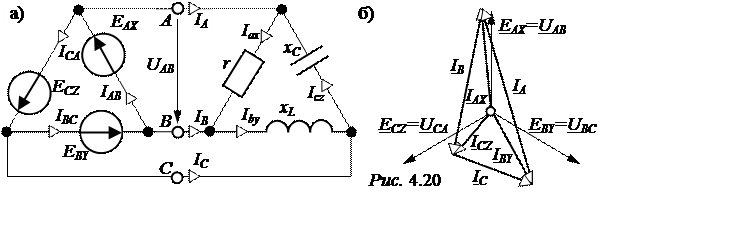
ЗАДАЧА 4.17. Схема задачи 4.16 питается от симметричного источни-ка, фазы которого соединены в треугольник. Считая источник питания идеаль-ным (рис. 4.20,а), фазную ЭДС Е_АХ = 380 B, найти фазные токи генератора.

Решение

Так как внутренние сопротивления фаз трёхфазного источника питания равны нулю, то при любых токах нагрузки линейные напряжения

U_AВ = Е_АХ = 380 B,  U_ВС = Е_ВY = 380×e ^–j120°B,   U_СА = Е_СZ = 380×e ^j120°B;   что совпадает с линейными напряжениями схемы задачи 4.16, на основании расчётов которой линейные токи

I_A = 7,1 + j1,9 А;       I_В = -6,13 + j1,34 А;      I_С = -0,97 – j3,24 А.

Для расчёта фазных токов генератора составим систему уравнений Кирхгофа. По первому закону Кирхгофа для узлов

А) i_АВ – i_СА = i_А;      В) i_ВС – i_АВ = i_В.

Уравнение по второму закону Кирхгофа для контура, состоящего из фаз генератора, запишем, исходя из того, что внутреннее сопротивление фазы генератора Z любое, но для всех фаз одинаковое – симметричный генератор. Получим     i_АВ×Z+ i_ВС×Z + i_СА×Z= Е_АХ + Е_BY + Е_CZ.

У симметричного генератора  Е_АХ + Е_BY + Е_CZ º 0, поэтому

Z×(i_АВ+ i_ВС + i_СА) º 0 при любом внутреннем сопротивлении Z.

Таким образом, для расчёта фазных токов источника питания необходимо решить систему уравнений

i_АВ – i_СА = i_А;

i_ВС – i_АВ = i_В;

i_АВ+ i_ВС + i_СА = 0;

откуда с учётом  i_А+ i_В + i_С = 0 получаем:

i_АВ=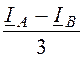;     i_ВС=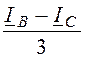;     i_СА=.  

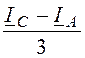Для рассматриваемого примера получаем:

i_АВ=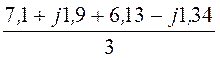= 4,41 + j0,19 А,              i_АВ= 4,41 А;

i_ВС=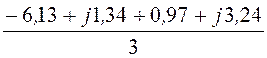= -1,71 + j1,53 А,     i_ВС= 2,3 А;

i_СА=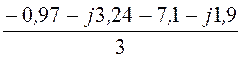= -2,69 – j1,71 А,          i_СА= 3,19 А.

Отметим, что фазные токи источника питания отличаются от фазных токов нагрузки, для которой на основании задачи 4.16 получено:

I_ax = 3,8 А;     I_by = 2,7 А;     I_cz = 3,8 А.

Векторная диаграмма токов источника питания приведена на рис.4.20,б.

ЗАДАЧА 4.18. Для питания осветительной нагрузки в опасных средах (угольная пыль и метан шахт, мукомольная пыль мельниц, цехи, обрабатывающие дерево, лакокрасочные производства и т.п.) применяется система треугольник-треугольник (рис. 4.21).

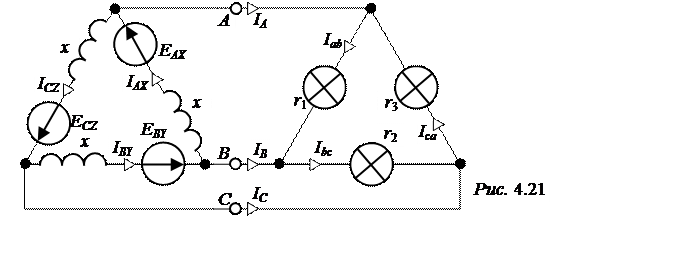Генератор симметричный, его фазные ЭДС   Е_АХ = E_ВY = E_СZ = 127 B, внутреннее сопротивление фазы x = 9 Ом. Нагрузка неравномерная, причём r₁ = 20 Ом, r₂ = 30 Ом, r₃ = 50 Ом. Рассчитать состояние цепи.

Решение

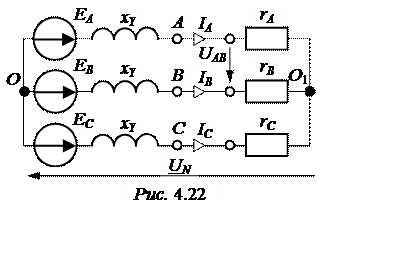
Преобразуем активный трёх-полюсник в эквивалентную звезду (рис. 4.22):

Е_А = E_В = E_С =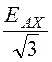== 73,3 B,

x_Y === 3 Ом.

Так же поступим и с нагрузкой. Сопротивления эквивалентной звезды