Трёхфазные цепи. Основные теоретические положения, страница 12

В результате проведенного преобразования источника ЭДС (последовательное соединение двух симметричных систем ЭДС – прямой и обратной последовательностей) схема в отношении симметричных составляющих симметрична и рассчитывается по методу наложения.

Расчёт тока прямой последовательности:

I₁ == =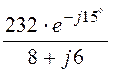 23,2×e ^–j51,87°А.

Расчёт тока обратной последовательности:

I₂ == =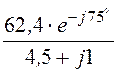 13,54×e ^–j87,53°А.

Токи в фазах двигателя рассчитаем с учётом того, что в трёхфазной трёхпроводной  системе  составляющие токов нулевой последовательности (I₀ = 0) отсутствуют:

I_А = I₁ + I₂ = 23,2×e ^–j51,87°+ 13,54×e ^–j87,53°= 35,10×e ^–j64,86°А,

I_В = a²×I₁ + a×I₂ = 23,2×e ^–j171,87°+ 13,54×e ^j32,47°= 12,22×e ^j160,95°А,

I_С = a×I₁ + a²×I₂ = 23,2×e ^j68,13°+ 13,54×e ^–j207,53°= 27,99×e ^j96,90°А.

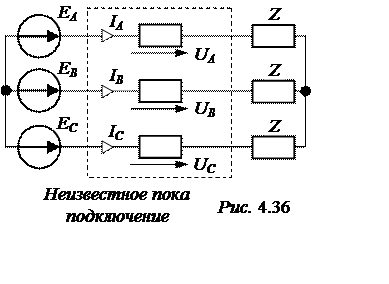
ЗАДАЧА 4.29. Двигатель зада-чи 4.28 был подключен к симметрич-ной трёхфазной цепи с линейным напряжением U= 380 B. В цепи про-изошёл обрыв линейного провода С.

Выполнить тот же расчёт, что и в задаче 4.27 для новых условий работы двигателя.

Решение

В симметричной трёхфазной цепи произошло продольное нарушение симметрии, что может трактоваться как последовательное подключение несимметричного приёмника с пока неизвестными напряжениями  U_А, U_В, U_С и токами I_А, I_В, I_С. Расчётная схема новых условий работы двигателя представлена на рис. 4.36.

Отметим, что в фазах неизвестного пока подключения могут содержаться как пассивные, так и активные элементы цепи.

Выполним формальное разложение несимметричных систем напряжений и токов подключения на симметричные составляющие.

U₀ =(U_A + U_B + U_C)                          I₀ =(I_A + I_B + I_C),

U₁ =(U_A + a×U_B + a²×U_C)     (1),        I₁=(I_A + a×I_B + a²×I_C),       

U₂ =(U_A + a²×U_B + a×U_C)                   I₂=(I_A + a²×I_B + a×I_C).

Определим симметричные составляющие заданной системы ЭДС генератора: по условию она остаётся симметричной, прямой последовательности при нарушении симметричного режима работы схемы.  Симметричная система ЭДС не содержит составляющих обратной и нулевой последовательности, то есть для ЭДС  E_A, E_B, E_C  получаем:

E₂ = E₀= 0;     E₁=== 220 B.

В отношении симметричных составляющих вся схема становится симметричной и её расчёт можно вести по схемам замещения для одной фазы применительно к каждой системе.

Схема замещения для тока прямой последовательности приведена на рис. 4.37,а, для тока обратной последовательности – на рис. 4.37,б, для тока нулевой последовательности – на рис. 4.37,в.

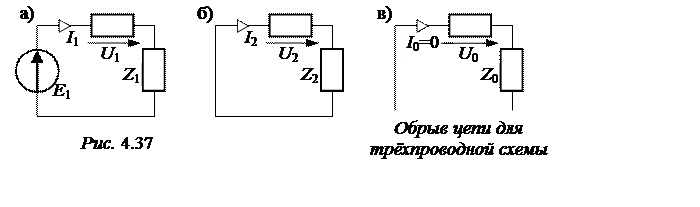В соответствии с законами Кирхгофа для схем замещения получаем 3 уравнения для определения шести симметричных составляющих неизвест-ных напряжений и токов:

I₁×Z₁ + U₁ = E₁;      I₂×Z₂ + U₂ = 0;      I₀ = 0.                                      (2)

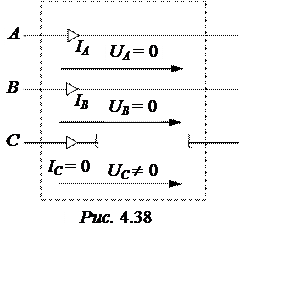Недостающие уравнения получим, исходя из характеристики несимметричности участка в соответствии с рис. 4.38 при обрыве линейного провода С:

;   ;   U_С ¹  0;

I_А ¹  0;       I_В ¹ 0;       .

Три подчеркнутых уравнения определённые. Перепишем их, заменив U_А, U_В, I_С  их симметричными составляющими (пока неизвестными):

U_A = U₀ + U₁+ U₂ = 0;

U_B = U₀ + a²×U₁ + a×U₂ = 0;                 (3)

I_C = I₀ + a×I₁+ a²×I₂= 0.

Из системы (1) с учётом того, что

U_А = 0,  U_В = 0 получаем

U₀ =U_С,   U₁ =a²×U_С,  U₂ =a×U_С,   откуда   = a.        (4)

Учтём, что  I₀= 0. На основании  (3) получаем

a×I₁ + a²×I₂ = 0, откуда    I₂ = -a²×I₁                 (5).

Оставшиеся уравнения (2) представим в виде

U₁ = E₁ – I₁×Z₁,   U₂ = -I₂×Z₂,   откуда с учётом (4) имеем

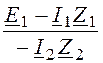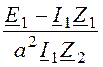== a,   а с учётом (5)   = a.

Так как a³ = 1, получаем   E₁ – I₁×Z₁ =  I₁×Z₂,   откуда

I₁ =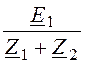==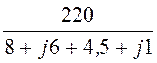 15,4×e ^–j29,25°А,

I₂ = -a²×I₁ = -e ^–j120°×15,4×e ^–j29,25° = 15,4×e ^j30,75° А,

I₀ = 0.

Токи в фазах двигателя:

I_А = I₁ + I₂ = 15,4×e ^–j29,25°+ 15,4×e ^j30,75°= 26,6×e ^j0,75°А,

I_В = a²×I₁ + a×I₂ = 15,4×e ^–j149,25°+ 15,4×e ^j150,75°= 26,6×e ^-j179,25°А,

I_С = a×I₁ + a²×I₂ = 15,4×e ^j90,75°+ 15,4×e ^–j89,25°= 0.