Что касается указанной мощности Рном, то надо сказать, что это – так называемая отпускная мощность, то есть мощность на валу у нагрузки-потребителя или мощность с учётом ещё и механического КПД двигателя.
В самом деле: Р =![]() ×UЛ ×IЛ×cosj=
×UЛ ×IЛ×cosj=![]() ×220×17,8×0,83 = 5629 Вт;
×220×17,8×0,83 = 5629 Вт;
Рном = Р×h= 5629×0,8 = 4504 Вт.
Поэтому в паспортных данных указывается либо h, либо Iном.
Параметры обмоток двигателя RФ, ХФ, ZФ определяют через расчётные электрические мощности. При соединении обмоток в треугольник:
UФ = UЛ =
220 В, IФ = IЛ/![]() = 10,28 А, РФ = Р/3
= 5629/3 = 1876 Вт.
= 10,28 А, РФ = Р/3
= 5629/3 = 1876 Вт.
 Тогда сопротивления обмоток:
Тогда сопротивления обмоток:
ZФ =![]() =
=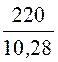 = 21,4 Ом;
= 21,4 Ом;
RФ =![]() =
=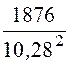 = 17,76 Ом;
= 17,76 Ом;
ХФ
=![]() =
=![]() = 11,95 Ом.
= 11,95 Ом.
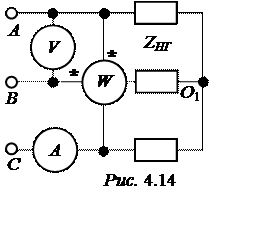
ЗАДАЧА 4.10. Симметричная нагрузка подключена к сети с напряжением 380 B(рис. 4.14). Амперметр показывает 2,2 А. Определить показание ваттметра, если:
а) ZНГ = RНГ; б) ZНГ = +jХНГ; в) ZНГ = -jХНГ.
Ответы: а) 0; б) –724 Вт; в) 724 Вт.
 ЗАДАЧА 4.11. Симметричная
нагрузка ZНГ =
10×e j45° Ом подключена к
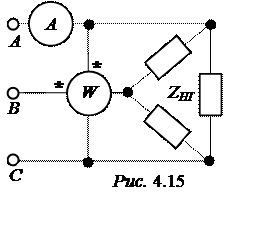
симметричному генератору (рис. 4.15). Определить показание ваттметра, если
амперметр показывает 17,3 А.
ЗАДАЧА 4.11. Симметричная
нагрузка ZНГ =
10×e j45° Ом подключена к
симметричному генератору (рис. 4.15). Определить показание ваттметра, если
амперметр показывает 17,3 А.
Ответ: -122,5 Вт.
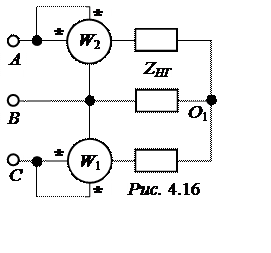
ЗАДАЧА 4.13. Для определения параметров симметричной трёхфазной нагрузки можно воспользоваться схемой Арона (схема включения двух однофазных ваттметров для измерения активной мощности трёхфазной трёхпроводной цепи) (рис. 4.16).
При UЛ = 220 В показания ваттметров – РW1 = 2128 Вт, РW2 = 570 Вт. Определить комплекс сопротивления нагрузки ZНГ.
Ответ: ZНГ = 9 + j9 Ом.
4.3. НЕСИММЕТРИЧНЫЕ ТРЁХФАЗНЫЕ ЦЕПИ
ЗАДАЧА 4.14. Определить токи в четырёхпроводной цепи (рис. 4.17,а) и напряжения на фазах несимметричного приёмника, включенного в симметричную трёхфазную сеть с напряжением U = 380 B, если
r
= wL
=![]() = 44 Ом.
= 44 Ом.
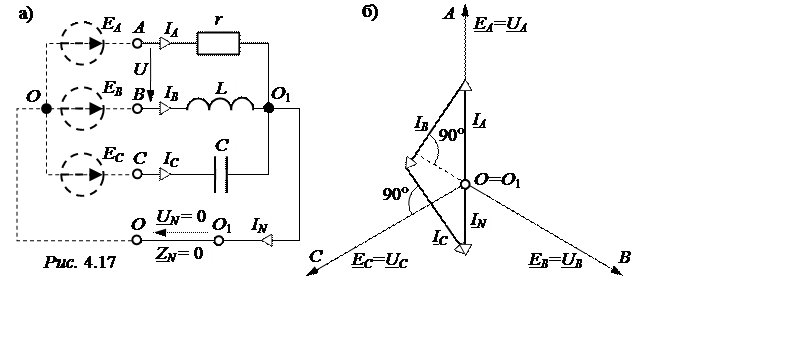
Найти активную и реактивную мощности
несимметричного приёмника, построить векторную диаграмму.
Решение
По умолчанию считаем, что фазы симметричного генератора соединены в звезду с выведенной нулевой точкой О (на рис. 4.17,а показано штриховыми линиями). Так как сопротивление нулевого провода ZN = 0, то потенциалы j0 = j01 = 0 и UN = j0 – j01 = 0.
В этом случае фазные напряжения несимметричного приёмника равны фазным ЭДС симметричного генератора UA = EA – UN = EA, аналогично UB = EB, UС = EС.
Фазная ЭДС E =![]() =
=![]() = 220 В.
= 220 В.
Приняв EA = 220 В, получим ЕB = 220×e -j120°B, ЕС = 220×e j120°B.
По закону Ома токи
IA =![]() =
=![]() = 5 А; IВ =
= 5 А; IВ =![]() =
=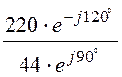 = 5×e –j210° А;
= 5×e –j210° А;
IС =![]() =
=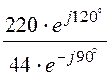 = 5×e j210° А, а по первому закону
Кирхгофа
= 5×e j210° А, а по первому закону
Кирхгофа
IN = IA + IВ + IС = 5×(1
+ e –j210° + e j210°) = 5×(1 -![]() )
= -3,64 A.
)
= -3,64 A.
Векторная диаграмма цепи приведена на рис. 4.17,б.
Активная мощность приёмника
Р = РА
+ РВ + РС =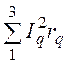 = IA2×r = 52×44 = 1100 Вт.
= IA2×r = 52×44 = 1100 Вт.
Реактивная мощность также определяется как алгебраическая сумма мощностей трёх фаз приёмника
Q
= QА + QВ + QС =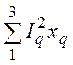 = IB2×wL
- IC2×
= IB2×wL
- IC2×![]() = 52×44 - 52×44 = 0.
= 52×44 - 52×44 = 0.
 ЗАДАЧА 4.15. Решить задачу 4.14 при разомкнутом нулевом
проводе.
ЗАДАЧА 4.15. Решить задачу 4.14 при разомкнутом нулевом
проводе.
Решение
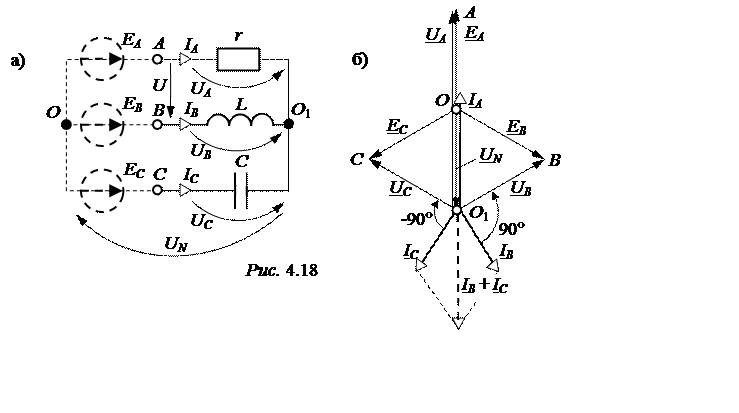
Приведём расчётную схему установки (рис. 4.18,а).
Рассчитаем узловое напряжение (напряжение смещения нейтрали)
UN=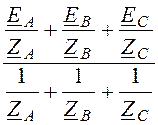 = 220×(1 + e –j210° +e j210°) = -160 B.
= 220×(1 + e –j210° +e j210°) = -160 B.
Фазные напряжения приёмника
UA = EA – UN = 220 + 160 = 380 B, UA = 380 B;
UB = EB – UN = 220×e –j120° + 160 = 50 – j190 B, UB = 196,5 B;
UC = EC – UN = 220×e j120° + 160 = 50 + j190 B, UC = 196,5 B.
Фазные токи приёмника равны линейным
IA =![]() =
=![]() = 8,64 A,
IA = 8,64 A;
= 8,64 A,
IA = 8,64 A;
IB =![]() =
=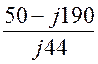 = -4,32 – j1,14 A,
IB = 4,47 A;
= -4,32 – j1,14 A,
IB = 4,47 A;
IC =![]() =
=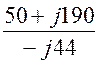 = -4,32 + j1,14 A,
IC = 4,47 A.
= -4,32 + j1,14 A,
IC = 4,47 A.
Проверка осуществляется по I закону Кирхгофа: IA + IВ + IС = 0, то есть выполняется.
Активная мощность приёмника
Р =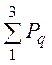 = IA2×r
= 8,642×44 = 3285 Вт.
= IA2×r
= 8,642×44 = 3285 Вт.
Реактивная мощность
Q
=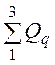 = IB2×wL
- IC2×
= IB2×wL
- IC2×![]() = 4,472×44 – 4,472×44 = 0.
= 4,472×44 – 4,472×44 = 0.
ЗАДАЧА 4.16. Рассчитать токи несимметричного треугольника (рис. 4.19,а), построить векторную диаграмму, если
U= 380 В,
r = xC = 100 Ом,
xL = 100![]() Ом.
Ом.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.