Трёхфазные цепи. Основные теоретические положения, страница 9

Сравнивая напряжения на фазах неповреждённых фаз при обрыве провода А  (U_B = U_C= 190 В)  и при работе в симметричном режиме, когда все напряжения  U_A = U_B = U_C = 220 В,  отмечаем уменьшение напряжения на 13,7%, что недопустимо для питания осветительной нагрузки.

Расчёт схемы при коротком замыкании фазы А осуществляется по общему правилу расчёта разветвлённой цепи с выполнением предельного перехода при  Z_A ® 0:

U_N=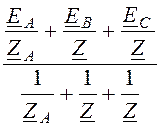==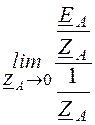 E_A.

Напряжения и токи неповреждённых фаз

U_B = E_B – U_N  = E_B – E_A = -U_AB = -380×e ^j30° = 380×e ^–j150° B;

I_B ===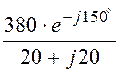 13,44×e ^–j195° A;

U_C = E_C – U_N  = E_C – E_A = U_CB = 380×e ^j150° B;

I_C ===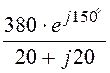 13,44×e ^j105° A.

Ток короткозамкнутой фазы

I_A ===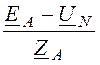= -(I_B + I_C) = -I_C ×e ^j30°= -23,3×e ^j135°= 23,3×e ^–j45° A.

выражение для  I_A  получено из условия, что для трёхпроводной системы  I_A + I_B + I_C = 0.

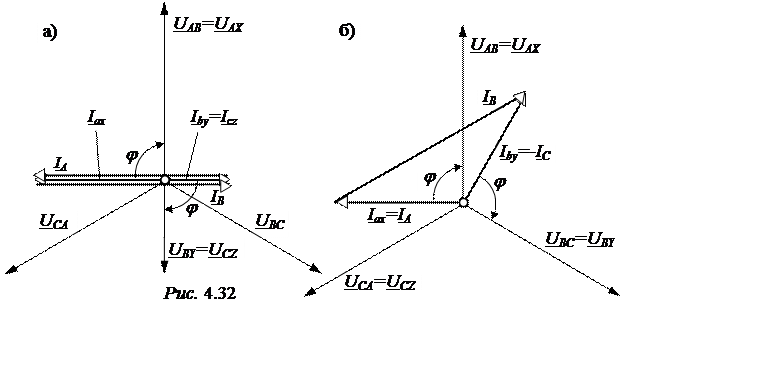
Векторная диаграмма цепи при коротком замыкании фазы А приведена на рис. 4.28,б.

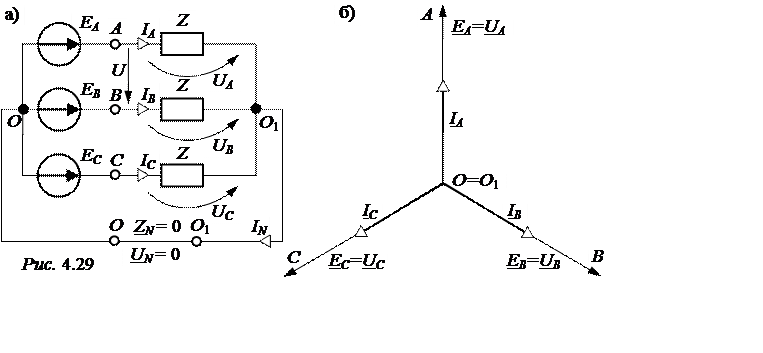
ЗАДАЧА 4.22. Для симметричной системы «звезда-звезда с нулевым проводом» (Z_N  = 0) (рис. 4.29,а) выполнить расчёты для трёх случаев:

- симметричный режим;

- обрыв линейного провода В;

- короткое замыкание фазы В,     если: U= 220 В,   Z = r = 20 Ом.

Решение

На рис. 4.29,б приведена векторная диаграмма для симметричного режима работы схемы, в которой   U_N = 0   из-за нулевого значения сопротивления  Z_N .

При этом фазные напряжения генератора и нагрузки одинаковы и в  раз меньше линейных напряжений:    U_Ф  = E === 127 B.

Примем E_A= U_Ф  = 127 B, тогда E_B= 127×e ^-j120°B,  E_С= 127×e ^j120°B;

 I_A === 6,35 А;  I_В = I_A×e ^–j120° = 6,35×e ^–j120° А;   I_С = I_A×e ^j120° = 6,35×e ^j120° А.    

При обрыве линейного провода Bможно считать, что последовательно с сопротивлением Z в фазу Bподключилось сопротивление обрыва Z_обр = ¥ и полное сопротивление ветви стало Z_В = Z + Z_обр = ¥. 

По II закону Кирхгофа для контуров «ветвь – нулевой провод» получаем при обрыве провода B:

I_A =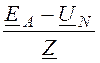=== 6,35 А  –  то же значение, что и при симметричном режиме,

I_В =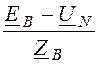=== 0;

I_С =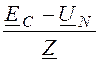=== 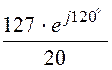6,35×e ^j120° А  –  то же значение, что и при симметричном режиме.

Ток нулевого провода

I_N = I_A + I_В + I_С = 6,35 + 0 + 6,35×e ^j120° = -6,35×e ^-j120° = 6,35×e ^j60° А. 

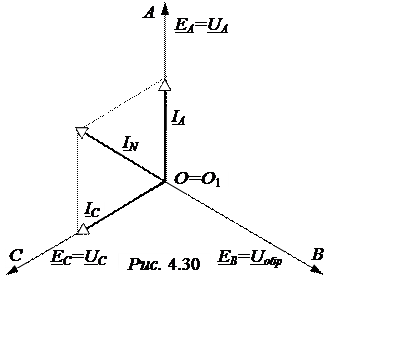
Заметим, что   I_N = -I_{В сим}.  По этому поводу говорят, что нулевой провод воспринимает на себя ток оборванной фазы. Векторная диаграмма цепи при обрыве провода Bприведена на рис. 4.30.

При коротком замыкании фазы Bв четырёхпроводной системе ток короткозамкнутого контура  E_B - Z_B - Z_N  неограниченно возрастает. Такой режим называется аварийным. Для защиты от такого аварийного режима в линейный провод B(и в остальные линейные провода) включаются плавкие предохранители, отключающие аварийную фазу (перегорают), после чего схема переходит в режим работы с оборванной фазой B(рис. 4.29).

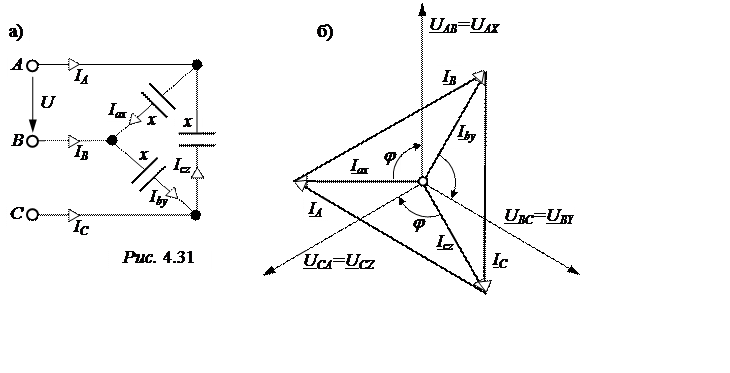ЗАДАЧА 4.23. Рассчитать режим работы симметричного треугольника (рис. 4.31,а) при  U= 660 В, x_C= 100 Ом  для четырёх случаев:

- симметричный режим;

- обрыв линейного провода С;

- обрыв фазы СZ;

- короткое замыкание фазы СZ.

Решение

Примем  U_AB = U = 660 B.

При соединении фаз нагрузки в треугольник его линейные напряжения равны фазным напряжениям. В симметричном режиме получаем

U_AX = U_AB = 660 B,    U_BY = U_BC = 660×e ^-j120° B,  U_CZ = U_СA = 660×e ^j120° B.

Фазные токи треугольника

I_ах =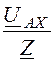==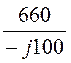 j6,6 = 6,6×e ^j90° А;

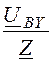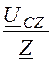I_by == I_ах ×e ^–j120° = 6,6×e ^–j30° А;     I_cz == I_ах ×e ^j120° = 6,6×e ^j210° А.    

Линейные токи треугольника

I_A = I_ах – I_cz =I_ах ×e ^–j30° = 11,4×e ^j60° А;

I_В = I_A×e ^–j120° = 11,4×e ^–j60° А;     I_С = I_A×e ^j120° = 11,4×e ^j180° = -11,4 А.     

Векторная диаграмма симметричного треугольника приведена на рис. 4.31,б. При обрыве линейного провода С все токи и напряжения нагрузки определяются только линейным напряжением U_AB.

Ток  I_ах =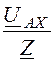==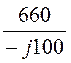 j6,6  А  - прежний.

Ток  I_С = 0, так как провод С оборван, токи

I_by = I_cz = -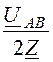= -= -j3,3  А,

напряжения на фазах     U_ВY = U_СZ = I_by ×Z = -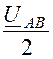= -330 B.