Трёхфазные цепи. Основные теоретические положения, страница 11

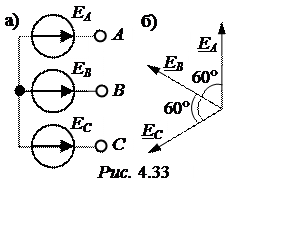
ЗАДАЧА 4.26. При соединении вторичных обмоток силового трёхфаз-ного трансформатора неверно были определены начало и конец обмотки BY. В результате соединения обмоток в звезду (рис. 4.33,а) система ЭДС приняла вид рис. 4.33,б.

Найти симметричные составляющие представленной несимметричной системы, если  E_A = E_B = E_C = 220 B.

Решение

Примем E_A = 220 B (рис. 4.33б), тогда

E_B = 220×e ^j60° B,   E_C = 220×e ^j120° B.

Составляющая нулевой последовательности

E₀ =(E_A + E_B + E_C) =(220 + 220×e ^j60° + 220×e ^j120°) =×e ^j60° = 146,7×e ^j60°B.

Составляющая прямой последовательности

E₁ =(E_A + a×E_B + a²×E_C),  где  a = e ^j120°,  откуда

E₁ =(1 + e ^j120°×e ^j60° + e ^-j120°×e ^j120°) == 73,33 B.

Составляющая обратной последовательности

E₂ =(E_A + a²×E_B + a×E_C) =(1 + e ^–j120°×e ^j60° + e ^j120°×e ^j120°) = 146,7×e ^-j60° B. 

Проверим результат разложения векторов на симметричные составляющие:

E_A = E₀+ E₁+ E₂= 146,7×e ^j60°+ 73,33 + 146,7×e ^-j60° = 220 B;

E_B = E₀+ a²×E₁ + a×E₂ = 146,7×e ^j60° + 73,33×e ^–j120° + 146,7×e ^-j60°×e ^j120° = 220×e ^j60° B;

E_C = E₀+ a×E₁ + a²×E₂ = 146,7×e ^j60° + 73,33×e ^j120° + 146,7×e ^-j60°×e ^–j120° = 220×e ^j120° B.

C

B

A

ЗАДАЧА 4.27. Из-за неравномерной нагрузки в конце трёхфазной трёхпроводной линии (рис. 4.34,а) напряжения образуют прямоугольный треугольник (рис. 4.34,б), катеты которого U_AB = U_BC = 360 B, причём синусоида линейного напряжения U_AB имеет начальную фазу на  больше синусоиды напряжения U_BC.

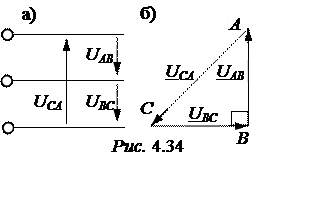
Определить симметричные составляющие несимметричной системы линейных напряжений. Найти коэффициент несимметрии.

Решение

Примем U_AB = U_AB = 360 B, тогда на основании рис. 4.34,б

U_BC = U_AB×e ^–j90° = 360×e ^–j90° B.

Так как линейные напряжения образуют замкнутый контур, то

U_AB + U_BC + U_CA º 0,  и  U_CA = -(U_AB + U_BC) = -(360 + 360×e ^–j90°) =

= -360×(1 – j) = 360×e ^j135° B.

Составляющая нулевой последовательности в линейных напряжениях отсутствует, так как  U₀ =(U_AB + U_BC + U_CA) =×0 = 0.

Составляющая прямой последовательности

U₁ =(U_AB + a×U_BC + a²×U_CA) =(360 + e ^j120°×360×e ^–j90° + e ^-j120°×360×e ^j135°) =

= 388 + j104 = 402×e ^j15°  B. 

Составляющая обратной последовательности

U₂ =(U_AB + a²×U_BC + a×U_CA) =(1 + e ^–j120°×e ^–j90° + e ^j120°××e ^j135°) =

= -28 – j104 = 108×e ^-j105° B. 

Коэффициент несимметрии    k === 0,269   или  k = 26,9%.

Заметим, что по Правилам технической эксплуатации установок потребителей (ПТЭ) степень несимметрии (коэффициент несимметрии) не должна превышать 4%.

ЗАДАЧА 4.28. К системе напряжений задачи 4.27 подключен соеди-нённый звездой асинхронный трёхфазный двигатель, каждая фаза которого имеет сопротивления: при прямом порядке чередования фаз Z₁= 8 + j6 Ом, при обратной последовательности –  Z₂ = 4,5 + j1 Ом. Найти токи в фазах двигателя.

Решение

Представим, что двигатель подключен к несимметричному генератору, а обмотки последнего соединены в звезду (рис. 4.35,а).

Рассчитаем симметричные составляющие фазных ЭДС несимметричного генератора, используя ранее найденные симметричные составляющие линейных напряжений U₁ и U₂ и их соотношения, представленные на векторных диаграммах рис. 4.35,б и 4.35,в:

E₁ =×e ^–j30° =×e ^–j30° = 232×e ^–j15° В;

E₂ =×e ^j30° =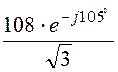×e ^j30° = 62,4×e ^–j75° В.

ЭДС несимметричного генератора выражаются через их симметричные составляющие:       E_А = E₁ + E₂ = 232×e ^–j15°+ 62,4×e ^–j75°= 268,7×e ^–j26,60° В,

E_В = a²×E₁ + a×E₂ = 232×e ^–j135°+ 62,4×e ^j45°= 169,6×e ^–j135°В,

E_С = a×E₁ + a²×E₂ = 232×e ^j105°+ 62,4×e ^–j195°= 268,7×e ^j116,6°В.