Трёхфазные цепи. Основные теоретические положения, страница 4

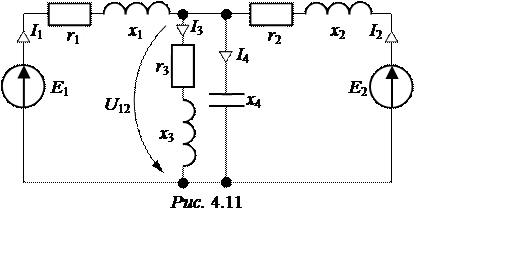
Построим  схему  замещения  трёхфазной  системы  для  одной  фазы (рис. 4.11). Фазные ЭДС рассчитаем по заданным линейным напряжениям в начале линий электропередачи  U₁ =U₂:     Е₁ = Е₂ ===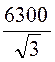 3638 В.

Так как эти напряжения при параллельной работе линий сфазированы, то начальные фазы у них одинаковы для соответствующих фаз. Примем

y_е1 = y_е2 = 0,    тогда комплексы ЭДС   Е₁ = Е₂ = Е₁ = 3638 В.

Комплексные сопротивления ЛЭП на фазу

Z₁ = r₁ + jx₁ = 0,5 + j0,3 Ом,   Z₂ = r₂ + jx₂ = 0,4 + j0,6 Ом.

Параметры присоединений рассчитаем по номинальным данным.

Для присоединения 3 получаем Р_Н =×U_Н ×I_Н ×cosj _Н, откуда

I_Н =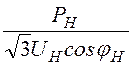==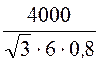 481 A;

полное сопротивление фазы при соединении нагрузки в звезду

Z₃ =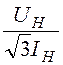==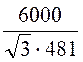 7,2 Ом;

активное сопротивление фазы нагрузки  r₃ = Z₃×cosj_Н = 7,2×0,8 = 5,76 Ом;

индуктивное сопротивление   х₃ =Z₃×sinj_Н =Z₃×= 7,2×0,6 = 4,32 Ом;

комплексное сопротивление     Z₃ = r₃ + jx₃ = 5,76 + j4,32 = 7,2×e ^j36,87° Ом.

Для батареи кон-денсаторов

Q_Н = 3×i_4Н ×x₄ =

=×U_Н ×I_4Н, откуда

i_4Н 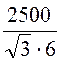 == 240,6 A;

х₄ ===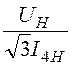

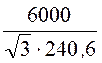= 14,4 Ом;

Z₄ = -jx₄ = -j14,4 Ом.

Расчёт схемы рис. 4.11 выполним методом узлового напряжения.

U₁₂ ==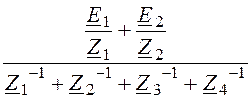

= 3638×=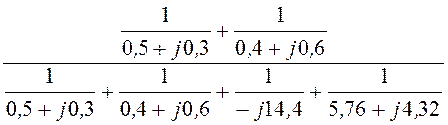

= 3530 – j72,8 = 3531×e ^-j1,18° B;

I₁ =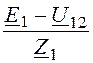==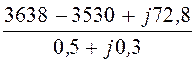 223,1 + j11,77 = 223,4×e ^j3,02° A;

I₂ =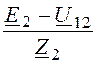==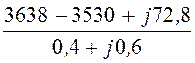 166,8 – j65,5 = 180,3×e ^–j22,23° A;

I₃ ===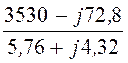 386,2 – j302,2 = 490,4×e ^–j38,05° A;

I₄ ===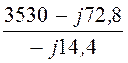 5 + j245 = 245,1×e ^j88,1° A.

Линейное напряжение на шинах подстанции

U_12л =U₁₂ =×3531 = 6115 B = 6,115 кВ.

Токи линий     I₁ = 223,4 A;   I₂ = 180,3 A.

Комплексные мощности источников питания (на входе ЛЭП)

S₁ = 3×E₁×= 3×3638×(223,1 – j11,78)×10^-3 = 2435 – j128,5 кBA,

S₂ = 3×E₂×= 3×3638×(166,8 + j65,5)×10^-3 = 1685 + j747,5 кBA, откуда     P₁ = 2435 кВт,    Q₁ = -128,5 квар,       S₁ = 2438 кBA;

P₂ = 1685 кВт,    Q₂ = 747,5 квар,        S₂ = 1843 кBA.

ЗАДАЧА 4.8. От Старобешевской ГРЭС в Донецк (60 км) необходимо передать мощность 3000 кВт при линейном напряжении у потребителя 35кВ

и  cosj= 0,8, но так, чтобы потери мощности в линии не превышали 5% от полезной.

Требуется рассчитать и сравнить затраты (например, меди) на сооружение однофазной 2-проводной и 3-фазной трёхпроводной ЛЭП.

Решение

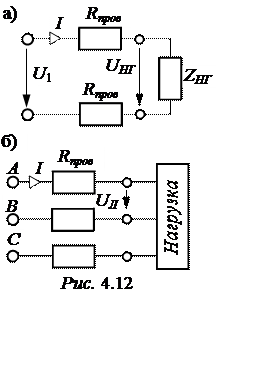
А. Однофазная линия передачи (рис. 4.12,а)

Дано: провода медные,  g= 5,7·10⁷ См/м,

l= 2×60 км,   r= 8,9 г/см³,   U_НГ = 35 кВ,

Р_НГ = 3000 кВт, cosj= 0,8, DР_Л = 5%Р_НГ = 150 кВт.

Требуется рассчитать вес меди, необходимой для проводов линии  G_меди - ?

Задача решается по следующему алгоритму:

I =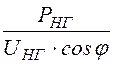==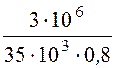 107 A;

R_пров =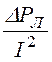==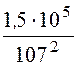 13,1 Ом;

S_пров =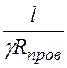==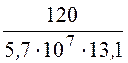 161·10 ^-6 м = 161 мм²;

G_меди = r ·l·S_пров = 8900·120·10³·161·10 ^-6 = 172000 кг = 172 т.

Б. Трёхфазная линия передачи (рис. 4.12,б)

Так как нагрузка симметричная, выполним пересчёт на одну фазу:

P_ф = Р_НГ/3 = 1000 кВт,   DР_Л = 50 кВт,   U_ф = U_Л/= 35/= 20,21 кВ.

Далее расчёт ведём аналогично:

I_ф = 61,9 A  ® R_пров = 13,1 Ом ®S_пров = 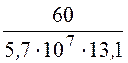= 80,4·10 ^-6 м = 80,4 мм²;

G_меди= 3·r ·0,5·l·S_пров = 3·8900·60·10³·80,4·10 ^-6 =129000 кг =129 т.

Заключение: по затратам меди на изготовление линии передачи 3-фазная ЛЭП экономичнее - G_3ф = 0,75G_1ф. Без доказательства – на 4-проводную линию уйдёт 87,5%G_1ф. И ещё: «звезда» по затратам меди втрое выгоднее «треугольника», но это уже из-за того, что при звезде придётся работать на более высоком напряжении.

ЗАДАЧА 4.9. Дано: двигатель типа

АК-52/4,   n = 1375 об/мин,   50 Гц.

Р_ном = 4,5 кВт,  U_ном = 220 В,

I_ном = 17,8 А,   cosj= 0,83,   КПД  h = 0,8.

Требуется определить сопротивления обмоток двигателя R_Ф, Х_Ф, Z_Ф.

Пояснения и решение

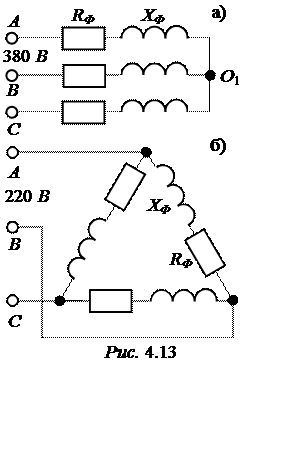
Прежде всего, следует помнить, что в паспорте электродвигателя указываются линейные величины напряжения  U_Л = U_номи тока I_Л = I_ном. Двигатель имеет три одинаковые фазные обмотки, сопротивления которых и требуется определить. Напомним ещё, что двигатели малой мощности выпускаются так, что их обмотки не соединены ни в звезду, ни в треуголь-ник. На клеммном щитке выведены 6 зажимов: начала обмоток А, В, С и концы Х, Y, Z. Чтобы получить указанную мощность двигателя, его обмотки можно соединить в звезду при напряжении 380 В (рис. 4.13,а) или в треуголь-ник, если в сети 220 В (рис. 4.13,б). Так что по условиям задачи можно заключить, что в нашем случае обмотки двигателя соединены в треугольник.