![]() - постоянная времени
дифференцирования
- постоянная времени
дифференцирования
3) Переходная функция
 |
![]()
4) Весовая характеристика
![]()
5) ЧХ
![]() ;
; ![]() ;
; ![]()
6) АЧХ
![]()
7) ФЧХ
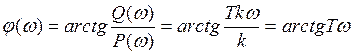
8)Годограф АФЧХ
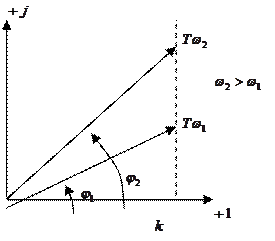 |
Вещественная не изменяется; мнимая изменяется, это показывает как будет изменятся годограф; годограф будет расти и совпадет с осью +j
9) ЛАЧХ
![]()
рассмотрим асимптотические распределения
1. ![]()
![]() , поэтому в формуле
, поэтому в формуле ![]() можно пренебречь
можно пренебречь
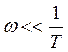
![]()
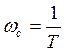
![]() - частота сопряжения
- частота сопряжения
![]()
2. ![]()
![]()
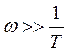
![]()
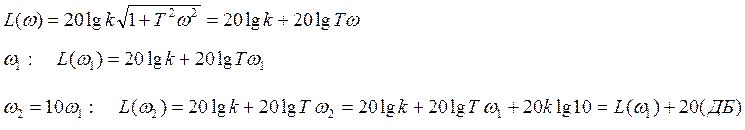
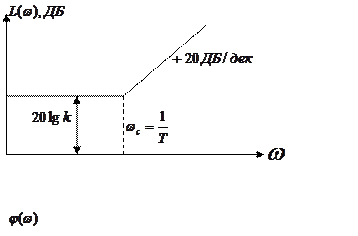 |
|||||
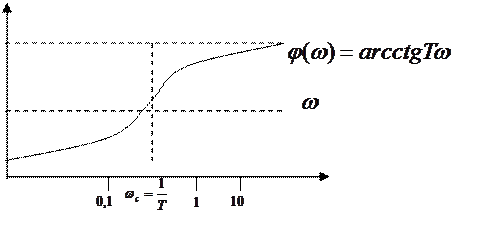 |
|||||
|
|||||
|
|||||
3.8 Колебательное звено (звено второго порядка)
1) 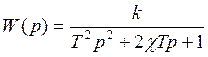 пропорциональное
звено
пропорциональное
звено
T – постоянная времени собственного колебания
![]() - коэффициент
демпферования
- коэффициент
демпферования
k – коэффициент передачи установившегося значения предполагается, что корни знаменателя – комплексные, т.е. нельзя разложить знаменатели на 2 корня первой степени
![]()
нам необходимо, что ![]() находится
от0 до 1:
находится
от0 до 1: ![]()
если больше единицы, то распадается на два действительных корня
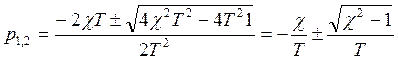
![]() Таким образом
Таким образом
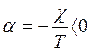 - действительная
часть
- действительная
часть
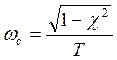 - мнимая часть
- мнимая часть
2) 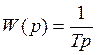 интегрирующее
звено
интегрирующее
звено
3) ![]() дифференцирующее
звено
дифференцирующее
звено
4) 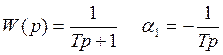 апериодическое
звено
апериодическое
звено
5) ![]() форсирующее
звено
форсирующее
звено
6) 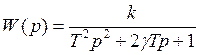 колебательное
звено
колебательное
звено
1)Колебательное звено
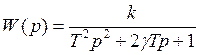
![]() - постоянная
времени
- постоянная
времени
![]() - коэффициент
демпфирования
- коэффициент
демпфирования
![]() - коэффициент
передачи установившегося значения
- коэффициент
передачи установившегося значения
демпфирование – гашение колебания
2) Дифференцирование уравнение
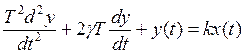
характеристическое ![]() уравнение
определяет поведение звена и полюса
уравнение
определяет поведение звена и полюса
1. ![]()
![]() ,
, ![]()
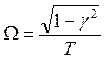
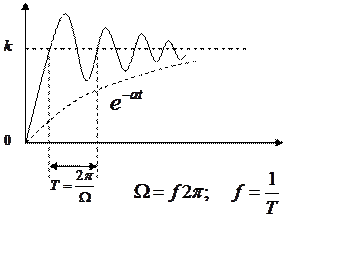
3) Переходная функция
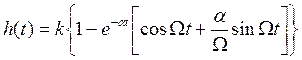
Чем ниже ![]() , тем быстрее
затухает процесс
, тем быстрее
затухает процесс
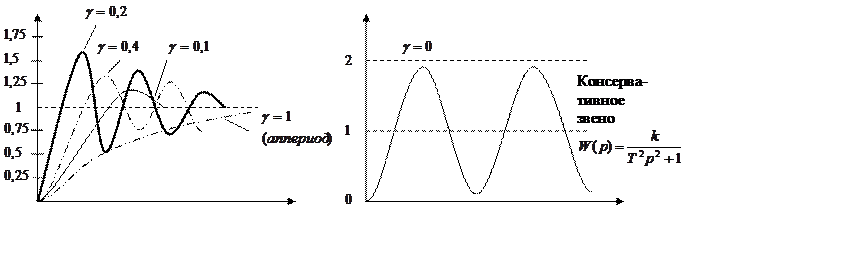 |
||||||||||
 |
||||||||||
|
||||||||||
|
||||||||||
|
||||||||||
4) Весовая функция
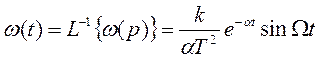
5) Чх
![]()
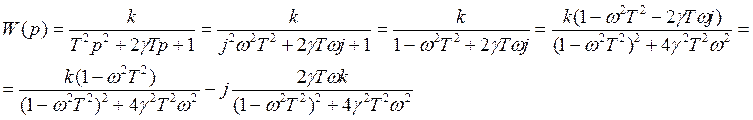
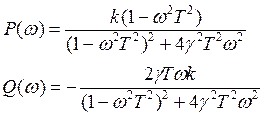
6) АЧХ
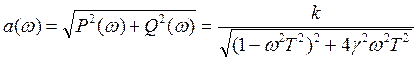
1. 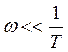 (низкочастотная
область)
(низкочастотная
область)
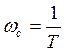 (сопряжение)
(сопряжение)
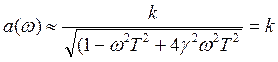
2. 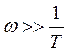 (высокочастотная
область)
(высокочастотная
область)
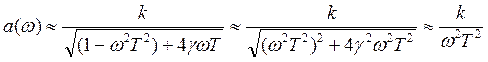
7) ФЧХ 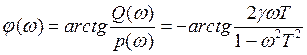
8) АЧХ
|
||||||
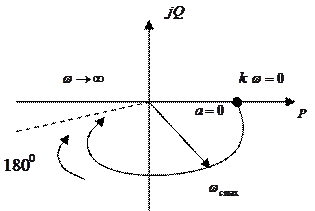 |
||||||
|
||||||
9) ЛАЧХ
![]()
1) 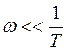
![]()
1) 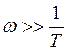
![]()
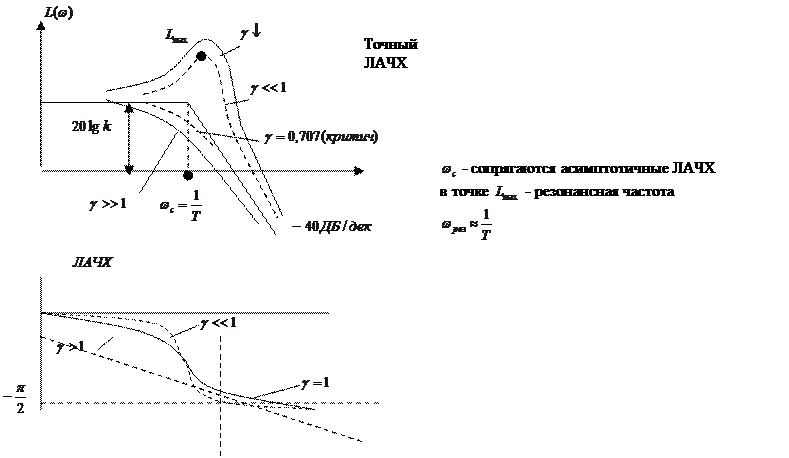 |
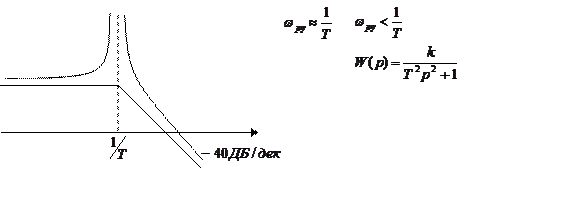
![]() - резонанс частоты
- резонанс частоты ![]()
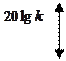 |
3.9 Звено чистого (транспортного) запаздывания
Сигнал, который воспринимает на выходе с задержкой ![]() - это линейное звено
- это линейное звено
Квазиалгебраическое уравнение не содержит производную
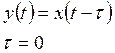 (1)
(1)
Принцип казуальности (причинности), которое запрещает ![]() : выходной сигнал не может появится
пока нет входного
: выходной сигнал не может появится
пока нет входного
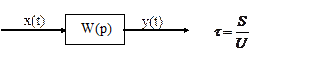 |
1) Передаточная функция
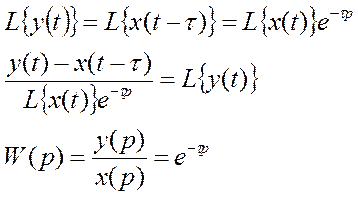
2) Переходная функция
если ![]() , то h(t) ,будет
в силу (1)
, то h(t) ,будет
в силу (1) ![]()
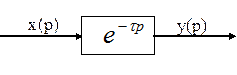 |
выходной сигнал от входного будет запаздывать на ![]()
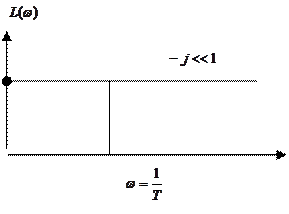
3) Весовая функция
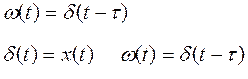
данная функция должна сопровождаться увеличением
аргумента, на самом деле ![]() функция выдается,
когда t=0, а нам нужно выдать при
функция выдается,
когда t=0, а нам нужно выдать при ![]() ,
тот и аргумент должен быть
,
тот и аргумент должен быть ![]()
![]()
![]()
 |
 |
![]()
![]() t
t
4) ЧХ
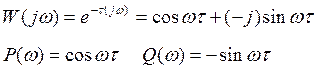
5) АЧХ
c каким усиление передается входной сигнал по амплитуде
![]()
двигает звено, но частота не изменяется
6) ФЧХ
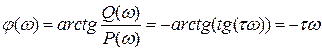
Фазовый сдвиг тем больше, чем больше частота
Если в ![]() укладывается 1
период, то задержание на 360
укладывается 1
период, то задержание на 360![]() и т.д.
и т.д.
7) АФЧХ (годограф)
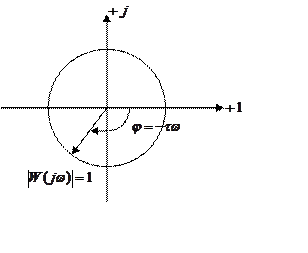 |
|||
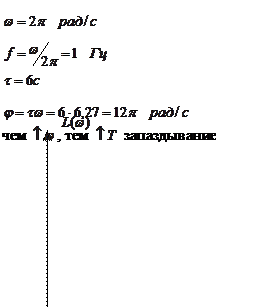 |
|||
|
![]()
|
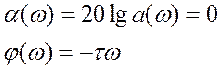
![]()
|
 тем
больше, чем больше
тем
больше, чем больше так как в логарифмическом масштабе,
то будет кривая.
4. Устойчивость линейных САУ.
Можно самостоятельно провести эксперимент.
Если мы возьмем 2 звена устойчивых и соединим на моделирование
![]()
![]()
|
|
![]()
![]()
![]()
![]()
![]()
на второй ненулевые условия, на выходе будет постоянный ненулевой сигнал
если мы замкнем обратную связь:
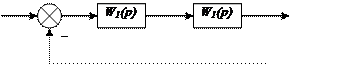
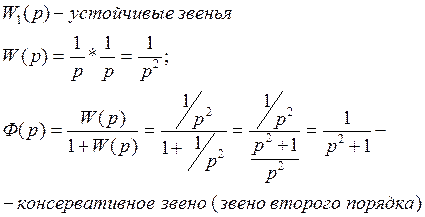
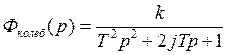
Начнутся незатухающие колебания при соединении обратной связи.

Система находится на грани устойчивости, но не работоспособна.
Свойство неустойчивости всплыло в регуляторах для паровой машины
Теперь проведем математический анализ, по которому сможем определить (спрогнозировать) будет она устойчивой или нет.
4.1 Формализованное понятие устойчивости.
Чтобы была понятна формулировка, вспомним дифференциальное уравнение
Все линейные звенья описываются уравнением (*),которое связывает входной и выходной сигнал и их производные
Если его решать, то решение будет следующим
Линейные автоматические дифференциальные уравнения выглядят следующим образом:
![]()

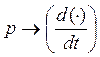
Y(t)=Yчастн(t)+Yобщ(t);
Yчастн– частное решение неоднородного ДУ (уравнения с правой частью);
Yобщ– общее решение однородного ДУ (уравнения без правой части).
Однородное
диф.ур. – исходное уравнение (*) с нулевой правой частью. Таким образом ![]() описывает поведение системы под
действием внутренних причин. Формально эти причины будут представлены
ненулевыми начальными условиями (заряд конденсатора, сжатой пружиной, ненулевой
скоростью моховых масс)
описывает поведение системы под
действием внутренних причин. Формально эти причины будут представлены
ненулевыми начальными условиями (заряд конденсатора, сжатой пружиной, ненулевой
скоростью моховых масс)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.