Основы теории автоматического управления. Основные термины и определения, страница 11

2. Замкнутая система устойчива, если ЛФЧХ разомкнутой системы на частоте среза имеет положительный запас по фазе, либо ЛАЧХ на частоте ω_s,  φ(ω_s)=180° имеет положительный запас по амплитуде.

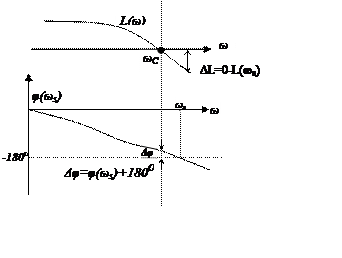
ЛАЧХ устойчивой системы

ω_С – частота среза

ΔL – запас по амплитуде (расстояние между нулем и значением ЛАЧХ)

Δφ – запас по фазе (расстояние между уровнем 180 и ЛФЧХ)

Если  направлена вверх, то положительный запас по фазе,  должна быть отрицательной.

    Рассмотрим пример неустойчивой системы

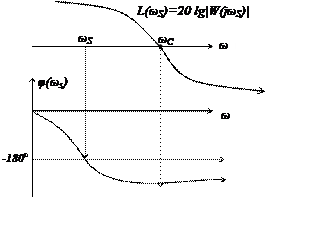
ЛАЧХ неустойчивой системы.

ω_S– частота, при которой φ(ω_S)=-180°

В режиме автоколебаний сигнал ошибки   можно считать синусоидальным

 - если колебания возникают, то возникают на границе среза.

 Предположим, что разом система находится в режиме автоколебаний, вносит фазовый сдвиг

   

Рассмотрим прохождение сигнала через разомкнутую систему.

Рассмотрим процесс суммирования сигналов на входе и выходе системы.

Инвертирующий сигнал y(t) совпадает со сдвигом на 180

Положительная обратная связь.

          

При суммировании обратная связь на этой частоте (ω_S) оказывается положительной. Сигнал усиливается за счет обратной связи:

    

Устойчивость системы на частоте ω_s  в условиях положительной обратной связи зависит от коэффициента усиления разомкнутой системы на частоте

   Проследим выполнение критерия Найквиста на графиках ЛФЧХ и ЛАЧХ устойчивой системы.

 На частоте возмущения колебания  там, где выполняется фазовых условиях самовозбуждения .

На ЛАЧХ эти условия отражаются в виде запаса по амплитуде,    , поэтому колебания будут затухающими.

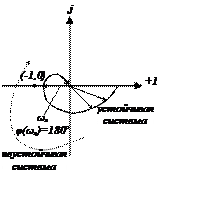
На уровне АФЧХ

   Пограничные условия автоколебаний соответствует положению годографа на частоте     

 Рассматриваем коэффициент передачи  . Если коэффициент > 1  годограф охватил эту точку  система неустойчивая. Если коэффициент < 1  система неустойчива, потому что коэффициент передаточной функции разомкнутой системы < 1.

Преимущества критерия Найквиста по отношению к другим критериям.

1) Возможность использования экспериментально-снятых частотных характеристик.

2) Возможность оценки устойчивости для систем, содержащих трансагентные иррациональные звенья.

Пример – звено частотного запаздывания, передаточная функция которого имеет вид ; для этого звена нельзя указать дробно-рациональное выражение, которое описывало бы это звено

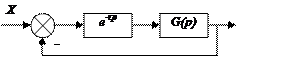
      поэтому спираль сжимается    

                                 

Если H охватывается спиралью система – неустойчивая, если не захватывается – устойчивая.

4.5.Построение ЛАЧХ разомкнутых систем

Пусть система состоит из прямого канала, в котором имеется последовательность звеньев. На входе сумматор, который позволяет суммировать

x(t)                                        

                                  

                                            Система разомкну

Чтобы получить общую функцию, нужно перемножить входные функции

Передаточная функция разомкнутой системы , но нас интересует ЛАЧХ   

 - коэффициент передачи АЧХ

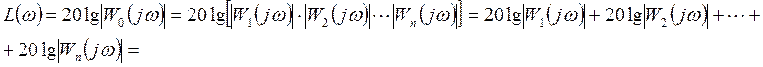
каждый элемент представляет ЛАЧХ элементарного звена

Чтобы найти ЛАЧХ разомкнутой системы нужно сложить ЛАЧХ каждого звена, входящего в прямой канал.

Пример 1.

Пусть прямой канал представляет

x(t)

форсирующее          интегрирующее

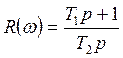 ПИ регулятора

тогда

20lgK                                                                                                                                                                                                                      ЛАЧХ                                          -20

+20

 - постоянная времени

Пример 2.

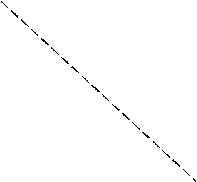
Построить ЛАЧХ двигателя постоянного тока, считая обратную связь по  разомкнутой.

Структура двигателя постоянного тока

20lg

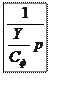
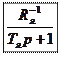
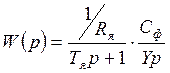
  В общем случае звенья могут быть большие

Домашнее задание.

Пример 3.

X                                                                                        y

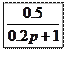
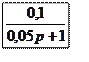
Ссылка на параграф 2.6 (построение оси частот)

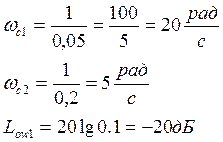
Построение результирующей фазо-частотной характеристики.

Каждое из звеньев вносит запаздывание, результирующее запаздывание будет суммарным:

Природа другая, не как у ЛАЧХ

Вид ФЧХ не очень красивый, так как отрезки кривых

x

склеиваем ФЧХ

90         45                                                                                                                                               -45        -90

фазовая характеристика для последовательного соединения.

5.Точность линейных автоматических систем.

5.1.Понятие точности САУ. Постановка задачи исследования точности.

Имеем автоматическую систему: прямой канал образован

x(t)                                            y(t)

                                                

 - характеристика точности

 получается как решение дифференциального уравнения (*) в общем случае содержит 2 компоненты

 - вынужденная составляющая, будем называть установившейся ошибкой, не обязательно в пределе = 0