Основы теории автоматического управления. Основные термины и определения, страница 4

          Т – период.(время, через которое

 значение функции повторяется )

¦=1/T -циклическая частота (число периодов в

 секунду)

w = 2p*¦  - круговая (угловая) частота. Угловая

частота показывает сколько периодов в радианной мере

укладывается в единицу измерения.

е. Обобщенный гармонический сигнал

Также синусоидальный сигнал, представленный в комплексной форме.

 k=a+jb – алгебраическая форма записи комплексного числа, где

 а- действительная составляющая

 jb- мнимая составляющая        

 

к=M(cos φ+jsin φ)-тригонометрическая форма записи комплексного числа

k=M*e^jφ- показательная форма записи комплексного числа

-длина вектора

φ=arctg b/a

                                         φ=ωt;      ω=2π/T;  b=M*cos φ=M*cos ωt

Формула Эйлера:

e^jφ= cos φ+jsin φ

 

X₁-синусоидальный,X₂-синусоидальный, но с другой амплитудой.

X₁=X_1mcos ωt

X₂=X_2mcos (ωt+ φ)

Представим входной сигнал в виде суммы двух комплексных чисел.

 

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                            

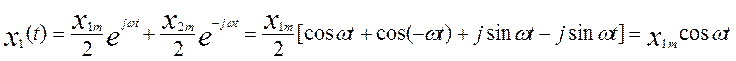
Представим аналогично другой сигнал:

   

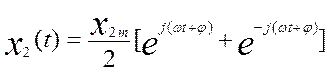
Сумма сигналов равна  сумме отклонений сигналов.

Представление входных и выходных сигналов в виде суммы двух входных сигналов и откликов позволяет полагать, что если на входе действует комплексный сигнал e^jωt, то на выходе будет сигнал e^{j(ωt+ φ)}                                                     

2.3 Преобразование Лапласа и его свойства.

В этом разделе даны основные сведения о преобразовании Лапласа, которые будут использованы при рассмотрении систем, описываемых линейными дифференциальными уравнениями.

                                  Пусть дана непрерывная функция f(t)

                                   Имеет ограничения:

                                   1. t<0=0

t

                                   2. Условие абсолютной сходимости

                                                     

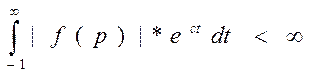
с-константа абсолютной сходимости.

Все типовые сигналы ему удовлетворяют.

Назовем функцию F(p) изображением по Лапласу от функции f(t),  если

                          F(p)=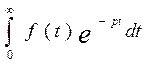   (1)

Для краткости следующую формулу записываем в виде:        

                                          F(p)=L{f(t)}  (2)      

Для типовых сигналов f(t) изображения вычислены и сосредоточены в таблице в приложениях по ТАУ.

p-оператор преобразования сигнала

j-комплексное число

p=α+jω-который можно интерпретировать как информационный ноль пробного сигнала:

X(t)=e- ^{α t}( cos ωt+ jsin ωt)

α-показатель затухания экспоненты

ω-частота

 Соотношения (1), (2) называют преобразованием Лапласа, ставящее Функции f(p) вещественного переменного в соответствие функцию F(p) комплексного переменного p (p= α+jω). При этом f(p) называют оригиналом, а F(p) называют изображением или изображением по Лапласу.

То, что f(p) имеет своим изображением F(p) или оригиналом F(p) является f(p), записывается так:

                                              f(t)F(p),

которое мы будем называть изображение по Лапласу.

Иногда также пользуются символической записью

                                                F(p)=L[f(t)]

Преобразование Лапласа является обратимым, т.е. по изображение может быть найден оригинал:

f(t)=L^-1[F(p)]=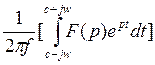

р – оператор преобразования Лапласа р=+jw, имеющий смысл комплексного независимого параметра

- показатель затухания пробного экспоненциального сигнала

w – круговая частота обобщенного гармонического сигнала

Пример: пусть f(t) имеет следующий вид: f(t)=1(t). Найдем изображение этого сигнала по Лапласу.

L[1(t)]=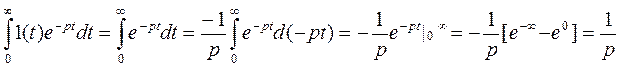

Обратные преобразования Лапласа.

ОРИГИНАЛ	ИЗОБРАЖЕНИЕ
1(t)
d(t)	1
t
tn
e-at
1- e-at
1-
sin wt
cos wt
e-at * sin wt
e-at * cos wt

Свойства преобразования Лапласа

·  линейность

f₁(t) F₁(p)

f₂(t) F₂(p)

тогда L(f₁(t)+ f₂(t))= F₁(p)+ F₂(p)

·     теорема о дифференцировании оригинала

Пусть известна функция f(t), ее производная (t)=df(t)/dt и ее изображение f(t)F(p). Если начальные условия нулевые, т.е. f(0)=0, то дифференцируемый аргумент в области изображений сводится к умножению на p, поэтому на техническом уровне p называют символом дифференцирования при переходе к изображению. Тогда изображение производной может быть найдено по формуле L((t)]=pF(p); f(t)|_t=0.

·  интегрирование оригинала

  Интегрирование оригинала сводится к делению изображения на p

               

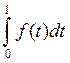
·  изменение масштаба по времени

   

·  смещение  аргумента у оригинала

f(t)  F(p)

Ф(р)-F(p)

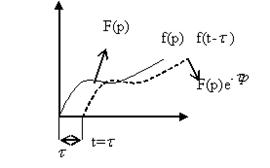
·  теорема о конечном  значении функции

f(t)  F(p)

·  теорема о начальном значении

f(t)  F(p)

2.3. Понятие передаточной функции

Передаточной функцией называют отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях. Если звено (система) имеет несколько входов, то при определении передаточной функции относительно какой-либо одной входной величины остальные величины полагают равными нулю.

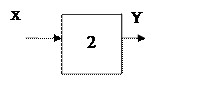Пусть нам нужно связать выходной сигнал с входным у некоторого элемента

Если можно ввести , что

                                                    , то мы