Другие предметы \ Теория автоматического управления

Основы теории автоматического управления. Основные термины и определения, страница 19

Форма кривой не изменяется при  любом ,  останется. Выбирая , мы можем сжимать или растягивать график.

В итоге:

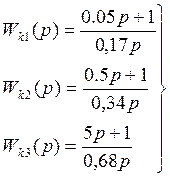
Мы получили 3 простых и однотипных регулятора вместо одного сложного, но для этого нужно три датчика.

7.2.7. Коррекция замкнутой системы с помощью п–регулятора.

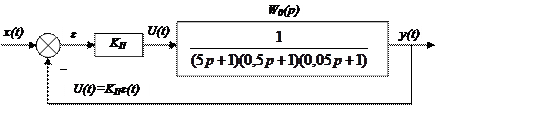
Такая система – статическая

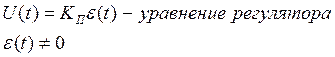
Предположим

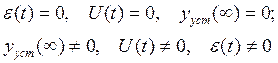
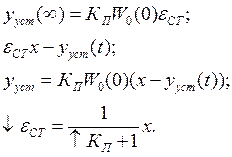
Убедимся, что увеличение КП уменьшает ошибку (εСТ)

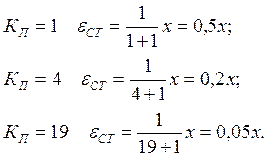
Рассмотрим влияние КП на динамические свойства системы

Построим ЛАЧХ разомкнутой системы:

          ΔL1=–41,6 дБ

Фазовая характеристика остается неизмен-ной, поэтому запас по фазе L2 уменьшается.

          ΔL2=–29 дБ

          ΔL3=6 дБ >0

Физика потери устойчивости при ↑Кп заключается в инерционности системы. Поэтому желательно скомпенсировать инерционность системы.7.2.2 Повышение быстродействия в разомкнутой системе.

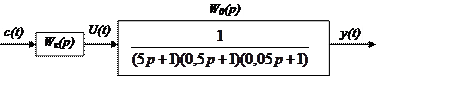
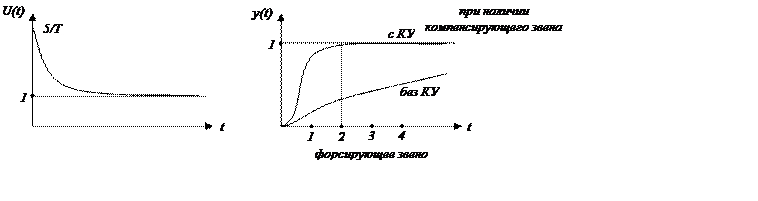
U(t)– корректирующий сигнал

c(t)– исходный сигнал

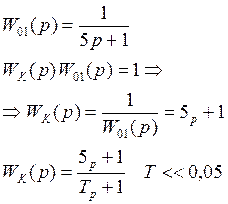
звено с наибольшей инерционностью

для реализации такой компенсации требуется форсирующее звено.

Введение фильтра в корректирующее устройство не изменяет свойств системы, если Т меньше наименьшей постоянной времени.

сокращение– компенсация

Рассмотрим физику работы корректирующего устройства

C(t)=1(t)      ступенчатая функция

 


8. Цифровые системы автоматического управления

Широкие возможности цифровых вычислительных машин позволяют использовать их в автоматических системах для достижения высоких показателей качества прочеса управления. Включение в контур управления цифровых вычислительных машин, хотя и требует дополнительных вспомогательных устройств, позволяющих осуществить преобразование непрерывных процессов в дискретные и обратное преобразование, компенсируется возможностью реализации практически любого закона управления, который делает всю систему в целом весьма эффективной.

          Структура аналогового регулятора

                                                                                  

                                                                             y
 

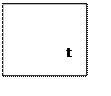
Подпись: t Подпись: ЗУ

Подпись: Д

Вычислительное устройство осуществляет преобразование информации на уровне формализованной оценки сигналов, то есть кодов . Все остальные операции преобразования информации сводятся к арифметическим действиям над кодовыми оценками сигналов.

Структура вычислительного управляющего устройства.

Отличие, что здесь появляется ЦАП и АЦП.

Чистый сигнал
 

AДC
 
 


M-ЭВМ работает по программе, реализуя многие функции которых не было в аналоговом преобразователе:

1)  Обслуживание датчиков (принять входной сигнал должна от датчика по программе);

2)  Обслуживание ЦАП;

3)  Обслуживание устройства индикации и управления.

Задачи аналогового:

  Алгоритмы цифрового устройства управления распадаются на две группы:

A.  Собственный алгоритм управления, который необходимо выполнять с жестко-заданной периодичностью периодом квантования (смотри далее интегральное регулирование). Однако в остальном математическое описание алгоритма этой группы полностью повторяет аналоговые алгоритмы. Это группа оперативных алгоритмов;

B.  Фоновые алгоритмы – обслуживают клавиатуру и индикацию, самодиагностика и т.д. Особенность: допустимо прерывание.

N*- означает параллельный вход, который может защелкнут в регулятор

Цифровой регулятор квантует выходные сигналы по времени

Структура управления программы

 


Период дискретности цифрового регулятора – время выполнения цикла управления программы. Т определяет момент времени выдачи управляющего кода от предыдущего.

1) , но  - этот эффект называют квантование (дискретизацией по времени)

T квантирует выдачу управляющего кода, т.е. является характеристикой кода.

В аналоговой системе такого кода нет

  

                  

                              
 
Диаграмма загрузки процессора будет выглядеть следующим образом:

 


2
 

2
 

t
 
 


                               

На диаграмме особенность: дискретный характер сигнала. В течение периода квантования T сигнал остается постоянным                  

2) Квантование по уровню

Входные и выходные устройства цифрового регулятора содержат регистры. Вследствие этого вх и вых информация разделена на порции – кванты.

Вес младшего разряда определяет квант – порцию информации

 


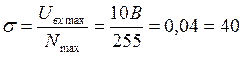Шаг квантования млВ

«-» эффект квантования по уровню ухудшается качество цифровых систем.

«+» возможность реализации сколь угодно сложных алгоритмов управления. При усложнении алгоритма аппаратура не меняется как в аналоговых.

8.1 Математическое описание звеньев цифровой системы

Математическое описание элементов, дискретных по времени производится с помощью аппарата родственному преобразованию Лапласа.

Дискретное преобразование Лапласа (z - преобразование)

Дискретное преобразование Лапласа (ДПЛ) мы будем называть величиной x(z) формулой регуляции по следующему закону:

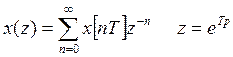   , где

Т- период дискретности

x[nT] – решетчатая функция, полученная путем выделения ее значений в дискретные моменты времени x(t)x[nT]

Переход от оригинала к изображению по Лапласу

Скачать файл