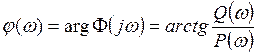
Круговая
частота ![]() является переменной.
является переменной.
Конец
радиуса вектора является комплексной характеристикой ![]() будет
поворачивать кривую на плоскости.
будет
поворачивать кривую на плоскости.
Геометрическое
место точек (ГМТ) конца вектора ![]() при изменении
частоты в этих пределах будет называться годографом Найквиста (просто
годограф).
при изменении
частоты в этих пределах будет называться годографом Найквиста (просто
годограф).
Свойства частотной характеристики.
Пусть для фиксируемого значения частоты обобщенный сигнал Х проходит через звено с частотной характеристикой W(jw), тогда
![]() X = X max ejwt
X = X max ejwt
Х – амплитуда синусоидального сигнала
Y – выходной сигнал
Y = Y max ej(wt+j) (Y – амплитуда, j - фаза),
Тогда W (jw) º ![]() =
=
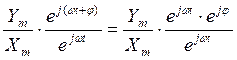
Частотная характеристика представляет собой комплексное
W (jw) = A(w)ejj число А(w) и фазой j, причем А(w) – модуль частотной характеристики.
А(w) = ![]() , j(w) – разность фаз: j(w)=jY - jХ.
, j(w) – разность фаз: j(w)=jY - jХ.
Таким образом, частотная характеристика показывает как изменяется амплитуда входного сигнала при прохождении через звено и как сдвигается фаза входного сигнала в функции частоты.
А(w) – амплитудно–частотная характеристика (АЧХ).
j(w) – фазовая частотная характеристика.
 |
 |
||
Частотную характеристику можно снять экспериментально:
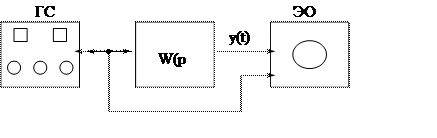 |
x(t) = Xm
y(t) = Ym sin (wt+w)

|
w |
w1 |
w2 |
wn |
|
Y |
Y1 |
Y2 |
Yn |
|
tt |
t1 |
t2 |
tn |
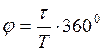
W(jw) = P(w) + jQ(w)
ВЧХ: P(w) МЧХ: Q(w)
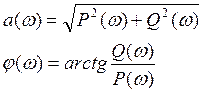
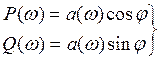
Представим ВЧХ как вектор на комплексной плоскости:
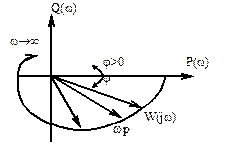 Назовем годографом (АФЧХ) частотные характеристики это геометрическое
место концов вектора частотной характеристики при изменении w = 0…¥
Назовем годографом (АФЧХ) частотные характеристики это геометрическое
место концов вектора частотной характеристики при изменении w = 0…¥
Годограф частотной характеристики – геометрическое место концов векторов частотной характеристики при изменении частоты от 0 до ¥
5. Логарифмические амплитудно – частотные характеристики (ЛАЧХ).
Логарифмические фазовые частотные характеристики (ЛФЧХ).
Кроме вышеперечисленных частотных характеристик используют еще логарифмические частотные характеристики (ЛЧХ) – логарифмические амплитудные частотные характеристики (ЛАЧХ) и логарифмические фазовые частотные характеристики (ЛФЧХ).
При
построении ЛАЧХ по оси абсцисс откладывают частоту в логарифмическом масштабе:
на отметке, соответствующей значению ![]() , пишут само
значение
, пишут само
значение ![]() , а не значение
, а не значение ![]() , а по оси ординат -
, а по оси ординат - ![]() . ЛФЧХ строят аналогично.
. ЛФЧХ строят аналогично.
Единицей
![]() является децибел, а единицей
логарифма частоты в ЛЧХ – декада. Декадой называют интервал, на котором
частота изменяется в 10 раз. При изменении частоты в 10 раз говорят, что она
изменилась на одну декаду.
является децибел, а единицей
логарифма частоты в ЛЧХ – декада. Декадой называют интервал, на котором
частота изменяется в 10 раз. При изменении частоты в 10 раз говорят, что она
изменилась на одну декаду.
Ось
ординат при построении ЛЧХ проводят через произвольную точку, а не через ![]() =0. Частоте
=0. Частоте ![]() =0
соответствует бесконечно удаленная точка:
=0
соответствует бесконечно удаленная точка: ![]() при
при
![]() .
.
Назовем ЛАЧХ зависимость L(w) º 20 lg a(w)
L(w) – логарифмический коэффициент изменения по амплитуде (ДБ).
![]() 0,001 0,01 0,1 1 10 100 1000
0,001 0,01 0,1 1 10 100 1000
![]() -60 -40 -20 0 +20 +40 +60
-60 -40 -20 0 +20 +40 +60
![]()
![]()
Ослабление Усиление
Изменение амплитуды на 20 ДБ означает изменение сигнала в 10 раз.
 Построение ЛАЧХ в логарифмическом масштабе по госту:
Построение ЛАЧХ в логарифмическом масштабе по госту:
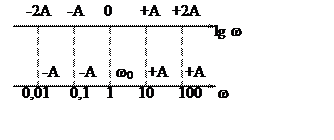 |
Зададим начало отчета w0 = 1
Отставание этой частоты от w0 будем изображать:
wх: 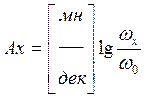 , А – масштаб логического представления
частоты.
, А – масштаб логического представления
частоты.
Порядок построения логарифмических частот:
1. выбрать начальную частоту (начало отчета w0 )нельзя принимать 0.
2. выбрать масштаб по частоте А, исходя из интервала частот, которые вы хотите представить, и размера рисунка
3. Разграфить ось частот пользуясь унифицированным соотношением
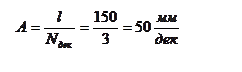
![]() w0 = 3дек
w0 = 3дек
l =150 mm
Декада – 10- кратное изменение частоты
Октава – 2- кратное изменение частоты
|
w |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0 |
0.3 |
0.48 |
0.6 |
0.7 |
0.78 |
0.85 |
0.9 |
0.95 |
1 |
ω=0 – точка в бесконечности.
Асимптотические ЛАЧХ – прямые, приближенно заменяющие криволинейные частотные характеристики при логарифмическом масштабе по амплитуде и частоте.
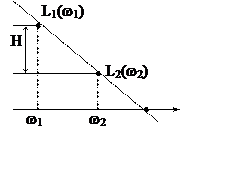 Наклон
асимптоты ЛАЧХ:
Наклон
асимптоты ЛАЧХ: 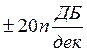 , n = 0,1,2,3…
, n = 0,1,2,3…
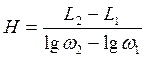
Диаграммы Боде:
ЛФЧХ особенность: ось ординат представляет фазовый сдвиг в номинальных единицах, в градусах, либо радианах.
ЛФЧХ совмещается с ЛАЧХ по оси Х..
 |
|||
 |
|||
t
3.Характеристики типовых линейных звеньев.
Выше мы определяли звено как математическую модель элемента. Вообще же звеном называют математическую модель элемента, соединения элементов или любой части системы. Звенья, как и системы, могут описываться дифференциальными уравнениями.
3.1.Типы соединения звеньев
 |
Последовательное соединение.
Найти эквивалентную передаточную функцию для последовательного соединения звеньев
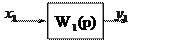 |
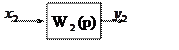 |
 |
![]()
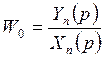 =?
=?
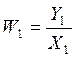 ,
, 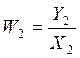 ,
…
,
… 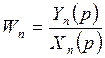
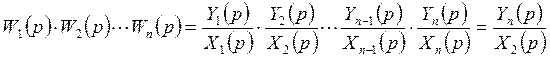
![]() ,
, ![]() …
…
![]()
![]() можно
сократить
можно
сократить
![]()
![]()
|
|
|
![]()
![]()
![]()
![]()
![]()
K1 K2 K3
![]()
Параллельное соединение.
|
 |
|||
![]()
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.