Основы теории автоматического управления. Основные термины и определения, страница 2

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                 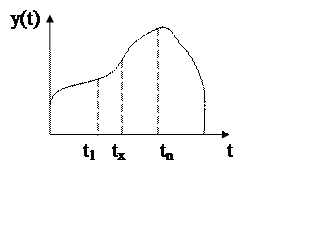Монотонность-между любыми двумя моментами времени t₁ и t₂        содержится сколь угодно много значений сигнала:

                                                                    t_xЄ(t₁,t₂)

                                                                     y(t_x)- !

Главной особенностью таких систем является то, что

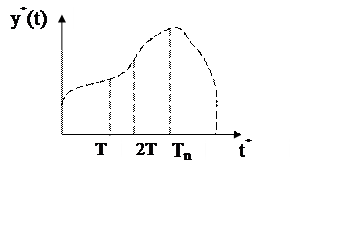
                                                                                              t_xЄ(T,2T,…,nT)

                                                                                              y*[nT]- !,

а для промежуточных значений y(nT) нет-это описание называется решетчатой функцией.

Историческая справка.

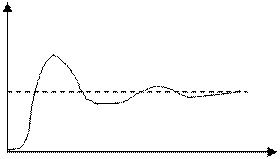
1784г. Первый опыт применил АС-центробежный регулятор Уайта. Оказалось, что паровая машина по своей природе не устойчива

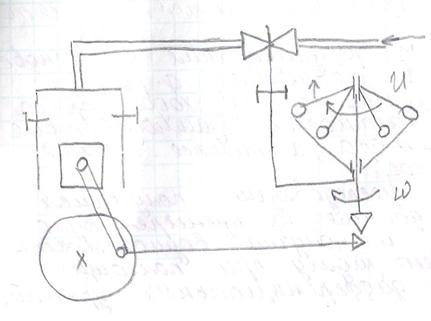пар от котла

Исходно двигатель стоит, грузики внизу, заслонка открыта, машина интенсивноразгоняется. По мере разгона машины скорость растет (w растет),  увеличивается, координата перемещения заслонки увеличивается следовательно заслонка закрывается.При одинаковых параметрах равновесное состояние не наблюдалось, следовательно, система оказалась неустойчивой. Природа неустойчивости в инерционности звеньев системы, что, в свою очередь приводило к запаздыванию сигнала.

 

                                                        

                                                  t                                                                t

Вышнеградский 1876г

М

                                              Все, что за линией  (внутри графика)          

                                                  относится к устойчивой системе. Все, что

                                             вне графика – к неустойчивой.

                                                 

                  «О регуляторах прямого действия»

Вышнеградский рассматривал процесс регулирования на основе динамики, учтя в уравнениях факторы, действительно существенные для хода процесса регулирования, в частности взаимодействие машины и регулятора, а также трение вязкое и кулоновское.

При дальнейшем исследовании полученных таким образом уравнений движения Вышнеградский пренебрег кулоновским трением и получил возможность рассматривать всю задачу при помощи теории линейных дифференциальных уравнений.

Пренебрежение кулоновским трением привело Вышнеградского к утверждению о необходимости для правильной работы регулятора снабдить последний «катарактом» - специальным поршнем, движущимся в цилиндре с маслом и создающим вязкое трение. Ожесточенная дискуссия, возникшая вокруг вопроса о необходимости катаракта, весьма способствовала выяснению многих положений теории регулирования, и появившиеся через несколько лет работы исправили эту ошибку Вышнеградского и показали, как нужно учитывать кулоновское трение. Однако, при учете кулоновского трения задача становится нелинейной и настолько сложной, что вплоть до самого последнего времени в общем случае оставалась нелинейной.

Образцовый анализ этой «линерализованной» задачи позволил Вышнеградскому сделать четкие технические выводы и установить знаменитые «неравенства Вышнеградского», которые с тех пор кладутся в основу расчета регуляторов. Эти неравенства были им наглядно представлены в виде так называемой «диаграммы Вышнеградского», вошедшей во многие, в том числе современные учебники; по прямоугольным осям этой диаграммы отложены безразмерные величины, пролсто связанные с практическими, конструктивными параметрами машины и регулятора; диаграмма указывает области устойчивой и неустойчивой работы системы машина – регулятор; более того, она показывает в устойчивой областиотдельно ту ее часть, которая соответсвует работе регулирующего устройства без всяких нежелательных колебаний.  

2. Математическое описание линейных систем

автоматического управления

Математическое описание –протекающих в системе, составленные на языке математики по физическим уравнениям. Для получения уравнения системы составляют уравнения для каждого входящего в него элемента. Совокупность всех уравнений элементов и дает уравнения системы.

Уравнения автомотической системы управления называют ее математической моделью. Математическая модель одной и той же системы в зависимости от цели исследования может быть разной, так как она должна, с одной стороны, как можно полнее отражать свойства оригинала, а с другой стороны, быть по возможности простой, чтобы не усложнять исследование.

Система управления и любой ее элемент производят преобразование входного сигнала x(t) в выходной сигнал y(t).

2.1 Линейные звенья автоматических систем

Существует некий оператор А, который ставит соответствие входному сигналу x(t) выходной сигнал y(t).

 Будем считать, что все звенья описываются дифференциальным уравнением, которое связывает входной и виходной сигналы.