Частное решение описывает вынужденное движение системы под действием входного сигнала при конкретном виде возмущения. Так как вид сигнала конкретный, поэтому решение частное.
С
точки зрения устойчивости, ![]() , так как она
описывает внутренние свойства, поэтому
, так как она
описывает внутренние свойства, поэтому ![]() в
теории управления принято называть свободной составляющей процесса
в
теории управления принято называть свободной составляющей процесса
Yобщ(t)–свободная составляющая (или переходный процесс), т.е.:
Yобщ(t)=Yсвобод.сост.(t)=Yпереход.пр.(t);
Yчастн–вынужденная составляющая (или полезная составляющая– управляет внешними сигналами):
Yчастн(t)=Yвынужд(t)=Yполезн(t).
Устойчивое движение системы– движение, в котором предел свободной составляющей при t→∞ равен нулю.
![]() Yсвобод(t)=0
(свободная составляющая затухает).
Yсвобод(t)=0
(свободная составляющая затухает).
4.2 Общие условия устойчивости для линейных систем.
Проведем рассмотрения, к коэффициенту уравнения типа (*), которые вытекают из условия устойчивости.
Однородное дифференциальное уравнение в области изображении (в оперантном виде) при нулевом входном сигнале
![]() (А)
(А)
Такое однородное дифференциальное уравнение имеет в общем случае решение в следующем виде:
Yсвобод(t)=c1eδ1(t)+c2eδ2(t)+…+cneδn(t);
![]() - постоянные интегрирования,
зависящие от начальных условий на
- постоянные интегрирования,
зависящие от начальных условий на ![]() и ее производные
и ее производные
δ1, δ2, δn – корни характеристического уравнения следующего вида:
a0 δn+a1δn-1+…+an-1δ1+an=0 – характеристическое уравнение
δi=α (действительные корни);
Yiсвобод=ciеδit=ciеαt; t– аргумент экспоненты.
Известно, что уравнение (***) имеет ровно n корней, где n – называют порядком системы
Так
как ![]() - действительные, то корни
- действительные, то корни ![]() могут быть либо действительными,
либо комплексно-сопряженными
могут быть либо действительными,
либо комплексно-сопряженными
![]()
![]()
Д.З.
: если мы умеем составлять уравнения
(А), умеем решать уравнения n – ой
степени, мы можем сказать: будет ли сходиться (затухать) решение ![]()
Рассмотрим
компоненты свободной составляющей, их вид зависит от корня характеристического
уравнения. Пусть ![]() , тогда вид этой компоненты
, тогда вид этой компоненты
![]()

α<0– затухание компонента свободной составляющей

α>0; Yсвобод=ciеαt
Можно
утверждать, что система устойчива, если все ![]() i=1…n
i=1…n
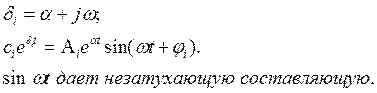
За затухание i-ой компоненты ответственен еαt.
НО! Может существовать вырожденный случай, когда два корня компенсируют друг друга
Есть
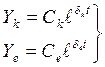 они дают взаимоуничтожающие решения
они дают взаимоуничтожающие решения
![]()
![]()
![]()
![]()
![]()
![]()

![]()
Это жесткие системы автоматического управления, которые могут существовать, но ограниченное время. С ростом времени из-за расхождения параметров системы рано или поздно одна из компонент забегает вперед, другая отстает. Такие системы используются для оборонной системы.
Вывод: при действительных корнях характеристического уравнения система устойчива тогда и только тогда, когда все корни находятся в левой полуплоскости
![]() +j
+j
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рассмотрим комплексно-сопряженные корени
![]()
Таким
корням будет соответствовать ![]() в силу
комплексно-сопряженных
в силу
комплексно-сопряженных ![]() и
и ![]() мнимые
части по формуле Эйлера уничтожаются =
мнимые
части по формуле Эйлера уничтожаются =![]() .
Синусоида определяется коэффициентом
.
Синусоида определяется коэффициентом ![]()
α<0 α>0
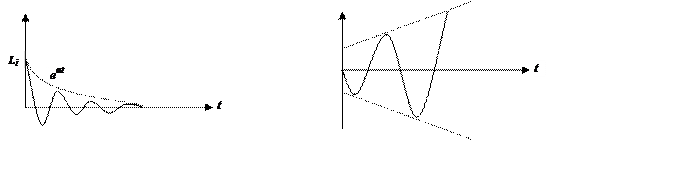
![]() определяет и обеспечивает затухание
определяет и обеспечивает затухание
Вывод: для комплексно-сопряженных корней верно то же утверждение: система устойчива тогда и только тогда и только тогда, когда корни характеристического уравнения расположены в левой полуплоскости (если находятся справа, то система неустойчива).
Корни должны обозначаться парами
![]()
![]() +j
+j
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Общее
условие устойчивости: для
устойчивости линейной системы необходимо и достаточно, чтобы действительные
части всех корней характеристического уравнения ![]() были
отрицательны. Иными словами, все корни характеристического уравнения должны
находиться в левой полуплоскости.
были
отрицательны. Иными словами, все корни характеристического уравнения должны
находиться в левой полуплоскости.
Характеристическое уравнение подразумевается для замкнутой системы, так как структура никак не оговаривалась.
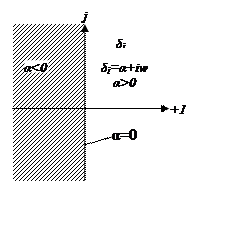
α=0– незатухающее колебание (система на грани устойчивости).
4.3 Алгебраический критерий устойчивости.
Методы, которые позволяют оценить устойчивость без решения характеристического уравнения.
Граничный случай , когда корни находятся на границе
Если
![]()
![]()
![]()
![]()
![]()
![]()
![]()
математически ![]() такая
система может существовать, но в жизни это не так.
такая
система может существовать, но в жизни это не так.
Алгебраический критерий Гурвица.
В
1895г. Немецким математиком А. Гурвица был разработан алгебраический критерий
устойчивости в форме определителей, составляемых из коэффициентов
характеристического уравнения системы. Смысл заключается в том, чтобы уменьшить
вычислительную работу и сделать решаемой уравнения 3, 4 и 5го порядка![]()
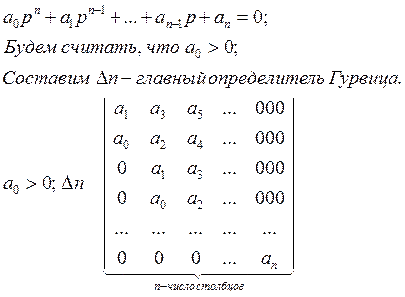
Определители Гурвица низшего порядка (диагональные миноры), выпишем их в явном виде:

всего
таких миноров можно указать ![]() . На этой базе мы
можем указать устойчивости
. На этой базе мы
можем указать устойчивости
Критерий
Гурвица: для того, чтобы система была
устойчивой, все определители Гурвица должны быть >0, т.е.: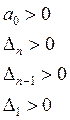
Пример система первого порядка:
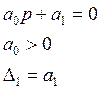
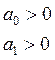
Пример система второго порядка:

4.4 Частотный критерий устойчивости Найквиста.
Этот частотный критерий устойчивости, разработанный в 1932г. Американским ученым Г. Найквистом, позволяет судить об устойчивости замкнутой системы по виду амплитудно-фазовой характеристики разомкнутой системы.
Пусть имеется
X(t) ![]() y(t)
y(t)

![]()
![]()
По передаточной функции можем получить частотную характеристику
![]()
![]()
что показывает комплексное число?
Модуль
АЧХ ![]() показывает отношение амплитуды
выходного сигнала к входному
показывает отношение амплитуды
выходного сигнала к входному
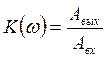
![]()
сдвиг фазы – показатель экспоненты ЧХ
![]()
Теоремы:
1. Замкнутая система устойчива, если годограф АФХ W(iw) разомкнутой системы не охватывает точку с координатами (-1, j0).
Устойчивая система.
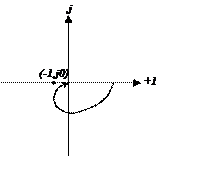

нет обратной связи
Неустойчивая система.

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.