![]() - свободная составляющая
- свободная составляющая
![]()
Точность регулирования – свойство САУ приближать выходной сигнал Y к входному при конкретном типе входного сигнала.
Количественной оценкой точности будем считать установившуюся ошибку, которую определим так
![]()
![]() зависит от входного сигнала
зависит от входного сигнала
5.2.Связь установившейся ошибки с передаточной функцией разомкнутой системы.
Преобразуем структурную схему системы к следующему виду:
|
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Передаточная функция по ошибке будет выглядеть следующим образом
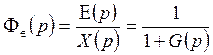
![]()
Разложим передаточную функцию по ошибке в ряд Тейлора в окрестности точки p=0
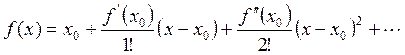
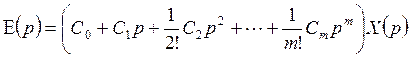
![]() - коэффициенты ошибки
- коэффициенты ошибки
![]()
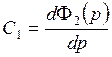
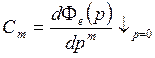
переходим от изображения к оригиналу
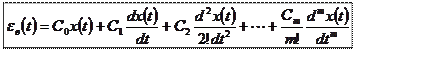
![]() Оль сигнала x(t) в
формировании ошибки
Оль сигнала x(t) в
формировании ошибки ![]() различную роль воздействия
входного сигнала и его производную.
различную роль воздействия
входного сигнала и его производную.
5.2.1.Статический режим.
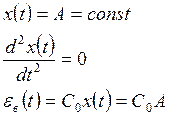
статическая ошибка при постоянном сигнале коэффициента статической ошибки
связь
![]() с передаточной функцией по ошибке
с передаточной функцией по ошибке
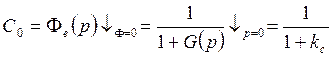
![]() - статический коэффициент передачи
разомкнутой системы
- статический коэффициент передачи
разомкнутой системы ![]() устанавливает статическую
ошибку в системе:
устанавливает статическую
ошибку в системе: 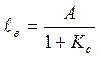
Системы,
у которых ![]() и
и ![]() называют
статическими системами, порядок астатизма q=0.
называют
статическими системами, порядок астатизма q=0.
Система, у которых ![]() ,
, ![]() -
астатические системы q>0/
-
астатические системы q>0/
Как
узнать по виду 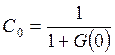 , чтобы G(0)
=
, чтобы G(0)
=![]()
Как сделать? Необходимо условие: наличие интегральных звеньев в разомкнутой системе.
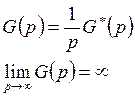
![]() - позиционная часть системы (не
содержит интегратор).
- позиционная часть системы (не
содержит интегратор).
Если система содержит хотя бы один интегратор, то она является астатической.
5.2.2.Изменение входного сигнала с постоянной скоростью.
|
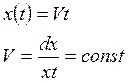

![]() =V
=V
![]()
![]()
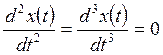
для
работоспособности системы ![]() , иначе ошибка
будет нарастаться
, иначе ошибка
будет нарастаться
![]()
полагаем,
что ![]()
![]()
![]() - ошибка от скорости
- ошибка от скорости
|

![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
q=1 q![]()
Система
с астатизмом II порядка содержит как min 2 интегратора, поэтому q![]() 2.
2.
Определим скорость ошибки для систем I порядка
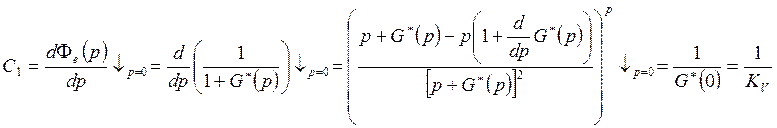
![]() - добротность системы по скорости
- добротность системы по скорости
![]() - статический коэффициент усиления
статической части разомкнутой системы
- статический коэффициент усиления
статической части разомкнутой системы
5.2.3.Режим изменения задающей величины с постоянным ускорением.
|
![]()

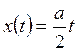
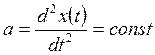 производная выше II
порядка равна 0
производная выше II
порядка равна 0
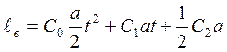
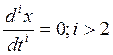
чтобы
![]() нужно С
нужно С![]() и
и
![]() =0
=0
установим
значение ошибки![]()
![]()
![]() - коэффициент ошибки от ускорения
- коэффициент ошибки от ускорения
|
![]()

![]()
![]()
![]()
Системы с астатизмом II порядка содержат 2 интегрирующих звена q=2
|
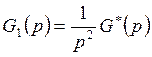


![]()
![]()
![]()
q>3 содержит как минимум 3 интегрирующих звена
Свяжем
![]() с передаточной функцией разомкнутой
системы
с передаточной функцией разомкнутой
системы
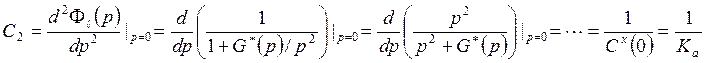
![]() - коэффициент усиления позиционной
части разомкнутой системы, добротность системы по ускорению
- коэффициент усиления позиционной
части разомкнутой системы, добротность системы по ускорению
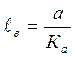 чем меньше
чем меньше ![]() , тем меньше ошибка.
, тем меньше ошибка.
5.2.4.Связь астатизма системы с ЛАЧХ разомкнутой системы.
Порядок астатизма – целое число q, которое равно порядку в описании входного сигнала, при котором установившаяся ошибка постоянна и отлична от нуля.
|
![]()
![]()
![]()
под этим рисунком подразумевается:
|
![]()
![]()
![]()
![]() y(t)
y(t)
![]()
![]()
Рассматриваем возмущение 3 видов:
|
![]()
![]()
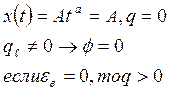
|
![]()
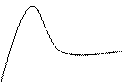
![]()
![]()
![]()
![]()
![]()
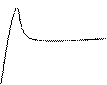
![]()
![]()
![]()
|
![]()
![]()
![]()
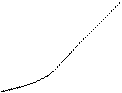

![]()
![]()
![]()


![]()
3. ![]()
|

![]()
![]()
![]()
![]()
![]()

![]()
Эти три эксперимента позволяют определить порядок астатизма системы. На практике астатизм второго порядка встречается редко.
5.2.5. Способы определения порядка астатизма.
Три способа:
1. По коэффициенту ошибок.
Вычислим несколько первых коэффициентов ошибок: ![]()
вычисление идет, пока необходим коэффициент, не равный нулю
Например: ![]() , то q=r
, то q=r
2. подсчет количества интегрирующих звеньев
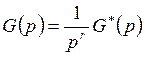
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.