Основы теории автоматического управления. Основные термины и определения, страница 17

 p₁, p₂, … , p_n – корни характеристического уравнения. Определяют поведение свободно – состоящей переходного процесса. Могут быть действительными, либо комплексно – сопряженными. Попарное сопряжение гарантирует отсутствие комплексной составляющей (j).

 (p- (a+ jb) ) × (p - (a- jb) ) = p² - p(a- jb) - p(a+ jb) +a² +b² = p² – p2a +a²+ b²

 

 Среднегеометрический корень характеристического уравнения:

Введем понятие среднегеометрического корня характеристического уравнения (А)

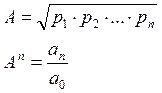 (обобщенная теорема Виета)

                    

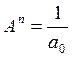
(вытекает из  по-

рядка астатизма)

Среднегеометрический корень позволяет ввести безразмерное время и сопоставить системы с различным быстродействием по одинаковой форме процесса. В относительном времени процессы в системах с одинаковым распределением корней будут выглядеть одинаково.

Преобразуем числитель Ф_жел и знаменатель Ф_жел.

Ф_жел(p) =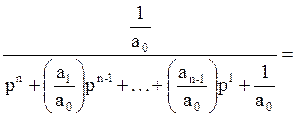

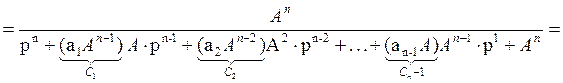
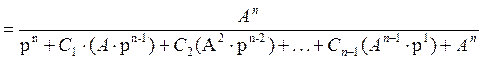
Сk=ak×An-k

                             

                      k = 1,2 … (n-1)

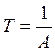 - базовая постоянная времени, обратная величина среднегеометрическому корню.

=(**) =

= (*)

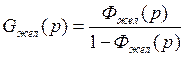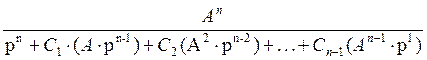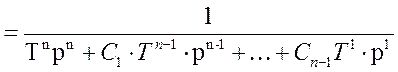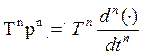
Введем относительное время t:

t =  (***), тогда

  =

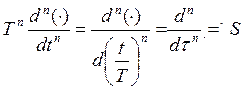
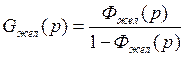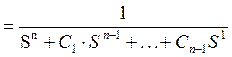
Видно, что переход к относительной времени позволяет оценивать переходный процесс по распределению корней характеристического уравнения, который задается коэффициентами С₁, С₂, … , С_n-1.

Обозначением S больше пользоваться не будем, снова вернемся к записи (*) и (**).

А и связанная с ним базовая постоянная времени Т(***) задают масштаб по времени.

Стандартизованное качество можно задать небольшим комплектом наборов коэффициентов С₁, С₂, … , С_n-1.

Порядок выбора желаемой переходной функции

1.  Определить порядок ? где  - порядок объекта

2.  Выбрать определенный способ распределения корней на комплексной плоскости. Этот способ будет определять вид переходных процессов.

3.  Определить коэффициенты  характеристического уравнения по способу распределения корней.

4.  Определить величину среднегеометрического корня (или базовую постоянную времени Т), исходя из требуемого быстродействия (время переходного процесса).

7.2.3.Аналитический синтез при биномиальном распределении корней.

При этом распределении все корни характеристического уравнения выбираются одинаково, действительные и –А.

p_i = p_j = -A           i¹j

 - бином Ньютона.

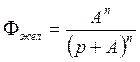
Геометрическая интерпретация:

 

Треугольник Паскаля.

Исследуем коэффициенты бинома Ньютона а₁, а₂, … , а_n-1 для различных порядков n.

                                                                                         Цифровые коэффициенты:                                                                                1

(p+A)¹ = p+A                           (n=1)                                        1        1

(p+A)² = p² +2Ap +A²              (n=2)                                     1       2        1

(p+A)³ = p³ +3Ap² +3A²p +A³ (n=3)                               1       3        3        1

                                                 (n=4)                             1               4       6        4              1

Желаемые передаточные функции различных степеней.

Порядок	Фжел(p)
1
2
3
4

Такие настройки задают свойства системы в относительном времени.

n	1	2	3	4
t п.п. (о.е)	3	4,75	6,3	7,8

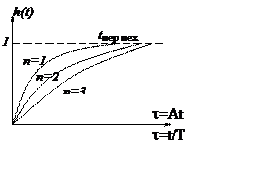
Т – выбирается на заключительном этапе проектирования, исходя изизаданного времени процесса.

                    п.п. – переходный процесс

                    о.е. – относительная еденица.

Свойство системы с бин. распределением корней:

Такая система гарантирует отсутствие перерегулирования и минимальное время при гарантировании монотонности процесса. Þ гарантирует необходимую точность. (процессы сборки, термостабилизации в медицине и т.д., Þ где важно не время работы, а монотонность).

Задание среднегеометрического корня производится из условия требуемого быстродействия переходного процесса.

Пример: порядок системы равен 3.

n=3              t_пп = 12.6 (сек)

                    t_пп = А* t_пп = 6,3 (о.е.)

                   

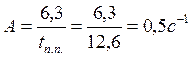
7.2.4. Аналитический синтез при распределении корней по  Батерворту. (Baterworth).

Настройки на модульный или технический оптимум.

Настройки на модульный (технический)  оптимум. При этом модуль частотной характеристики в окружности частоты среза (1 декада) является минимальным.

С математической точки зрения такое распределение характеризуется следующим: модули всех корней одинаковы  .

Сами корни располагаются на окрестности радиуса А в левой полуплоскости.

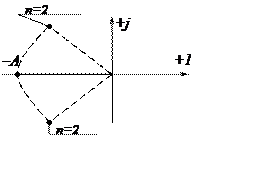 Если число корней четное, то расположение симметрическое, если нечетное, то один из корней раположен на мнимой оси, а остальные симметричны.

w		p(корни хар. ур).
1
2
3
4

Рассмотрим универсальные переходные функции системы

Универсальное распределение корней по Батерворт.

n=3

n=2

                                                                

 

                                                                  

 

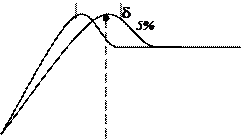так как универсальные, то зависят от относительного времени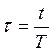

для  

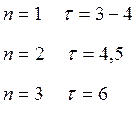
справочные данные удобно поместить в таблицу:

N	1	2	3	4
tm (о.е)	–	4,44	5	6,36
tп.п (о.е.)	3	3	6	7,2
d	–	4,3%	8,3%	6,2%