Рассмотрим связь между z-преобразованием и преобразованием Лапласа
 |
|||
|
|||
Время цикла – время, с которым она считывает и обрабатывает результаты
Z – оператор ДПЛ ![]() , где
, где
T- период квантования по времени
P – параметр непрерывного преобразования Лапласа
Связи дискретного преобразования Лапласа и непрерывного преобразования Лапласа.
Представим последовательность ![]() импульсов,
площадь которых пропорциональна значениям решетчатой функции
импульсов,
площадь которых пропорциональна значениям решетчатой функции
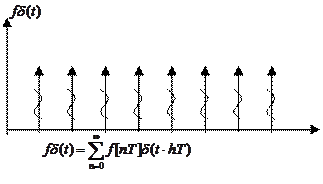 |
|||
|
|||
![]()
nT –
смещение ![]() функции
функции
Каждая функция ![]() при
изменении времени от 0 до
при
изменении времени от 0 до ![]() вносит эту сумму
в свой вклад 1 раз, когда время равно смещению.
вносит эту сумму
в свой вклад 1 раз, когда время равно смещению.
Возьмем обычные преобразование Лапласа
![]()
![]()
![]()
Например преобразование Лапласа
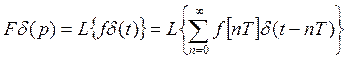
![]()
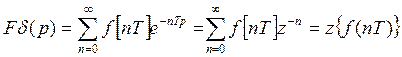
Таким образом мы можем утверждать, что обычное
преобразование Лапласа от последовательности импульсов ![]() промодулированной
значениями решетчатой функции и является ДПЛ
промодулированной
значениями решетчатой функции и является ДПЛ
Значительной разницы между преобразованием Лапласа и ДПЛ нет.
Необходимо пользоваться ДПЛ для того, чтобы для
математического описания цифровых систем выполнялось теми же средствами, что и
аналоговые системы. При этом сигналы в цифровых системах (коды) нужно представлять
себе последовательностью ![]() импульсов.
импульсов.
Таблица соответствия непрерывной функции обычного преобразования
Лапласа и z-изображения
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
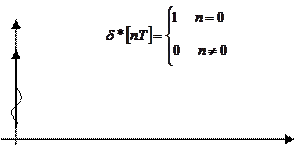 |
|||||
|
|||||
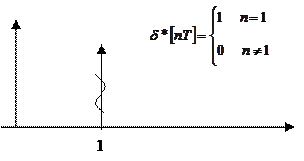 |
|||||
|
|||||
Основные свойства z-преобразования
1. Свойства линейности заключаются в том что преобразования от ∑ равен сумме отдельных преобразований функций.
![]()
2. Свойства сдвига оригинала во времени
![]()
Сдвиг оригинала на k-тактов в
сторону запаздывания приводит к умножению z-изображения на
![]()
3. Теорема о начальном значении оригинала
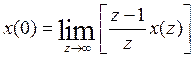
4. Теорема о конечном значении оригинала
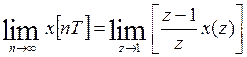
8.4Разностные уравнения
Представим себе цифровую систему управления, на входе которой действует решетчатая функция управления
 |
Чтобы связать входной и выходной сигналы нужно иметь средства. Для линейных алгоритм цифрового управления выходная последовательность кодов связана со входным разностным уравнением
|
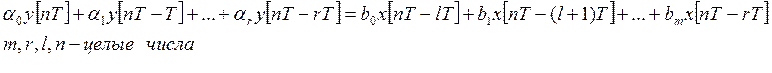 m, n, l, r – связаны
между собой следующим соотношением:
m, n, l, r – связаны
между собой следующим соотношением:
l=r-m
n – текущее дискретное время, которое указывает на последовательный сформированный регулятором отчет
|
![]()
![]()
![]()
Все линейные алгоритмы могут быть описаны таким разностным уравнением, поэтому оно имеет общий характер.
![]() приращение
функции
приращение
функции
Аналогично дифференциальному уравнению ![]()
Условие причинности, физическая реализуемость
![]() - будущие
значения переменных
- будущие
значения переменных
8.3 Дискретная передаточная функция
Дискретную передаточную функцию будем характеризовать цифровым устройством.
Выполним z-преобразование от левой и правой части разностного уравнения, при этом используем свойство линейности, поэтому в каждой части уравнения появляется сумма преобразования от слагаемого уравнения.
Кроме того, используется теорема о сдвиге оригинала, поэтому каждое слагаемое будет иметь множитель, отображающий сдвиг этого слагаемого
![]()
![]()
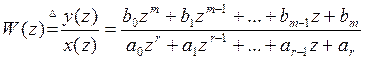
Понятие передаточной функции и дискретной передаточной функции введено только для нулевых начальных условий
Начальные условия будут выглядеть следующим образом
![]()
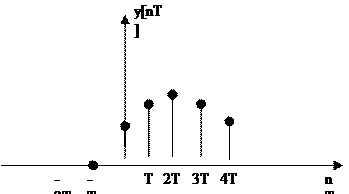 |
8.6 Переход от дискретного преобразования функции к разностному уравнению
Пусть задана дискретная передаточная функция в следующем виде и она описывается цифровым регулятором
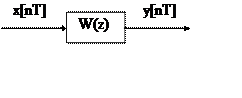
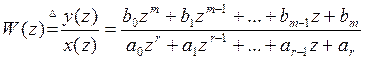
Получить алгоритм работы регулятора в виде разностного уравнения:
1) Преобразуем дискретную передаточную функцию
![]()
2) разделение на старшую степень знаменателя ![]()
Цель этого: получить в левой и правой части отрицательную степень:
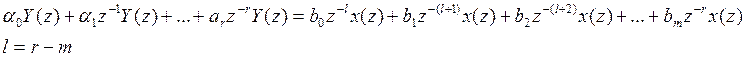
3) Переходим к оригиналам, используя теорему сдвига
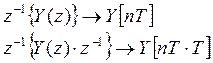
![]()
4) Выделим выходной сигнал на текущий момент времени
![]()
r – самый старший показатель
Регулятор имеет рекуррентный (возвратный) выходной сигнал.
Получим уравнение позволяющее рассчитывать выходной сигнал регулятора по коэффициенту дискретной передаточной функции и дискретным значениям входного и выходного сигнала задержанным на несколько тактов. Фактически это алгоритм работы цифрового регулятора.
8.5 Условие физической реализуемости цифрового регулятора
Обратим внимание на величину максимального сдвига
входного сигнала на величину сдвига ![]() , где
, где ![]() - старшая степень полинома
знаменателя ДПФ,
- старшая степень полинома
знаменателя ДПФ, ![]() - старшая степень
числителя.
- старшая степень
числителя.
Ясно, что ![]() должно быть
должно быть ![]()
![]() , означает
использование в алгоритме будущих значений входного сигнала.
, означает
использование в алгоритме будущих значений входного сигнала.
Требование ![]() , означает что
, означает что ![]() , т.е. старшая степень знаменателя
не меньше старшей степени числителя.
, т.е. старшая степень знаменателя
не меньше старшей степени числителя.
8.6 Пример расчета переходного процесса в дискретном звене (регуляторе).
Аппарат ДПФ удобно использовать для расчета переходного процесса, так называемым разностным методом.
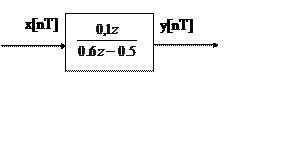 |
Найти: уравнение алгоритма такого звена и построить переходную функцию, т.е. реакцию на дискретное единичное ступенчатое воздействие
![]()
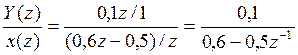
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.