Основы теории автоматического управления. Основные термины и определения, страница 14

Таким образом амплитуда определяется показателем .

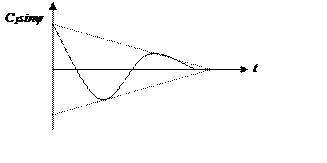
Например: при перемещении корня по лучу, исходящему из координатного угла, показатель колебательности сохраняется и форма переходного процесса не изменяется.

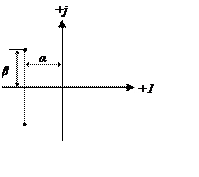
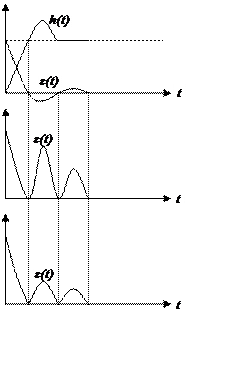
 Сделаем рисунок, который подтверждает вышесказанное

Для обоих пар корней 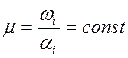 , время переходного процесса изменяется, а вид не изменяется

Y                                                           t

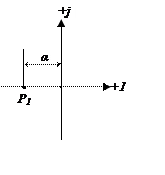
Вариант 1.

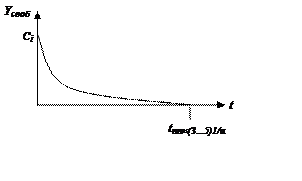
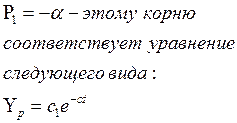
Вариант 2.

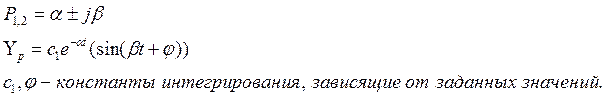
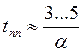– не учитывает форму переходного процесса.

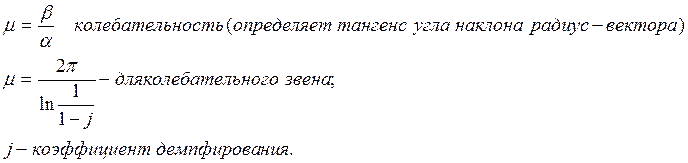
Примеры влияния положения координат на характер переходного процесса.

1. Корни перемещаются в горизонтальной оси.

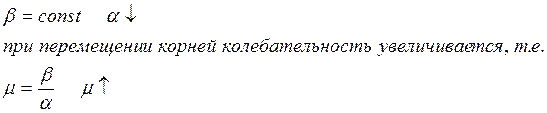
2. Корни перемещаются в вертикальной оси.

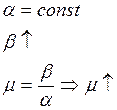
3. Перемещение корней по радиусу.

	α=const

`

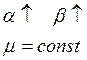α и β увеличиваются пропорционально, μ остается неизменной.

При этом не меняются амплитудные показатели качества, т.е.:

2– сжат по оси времени.

Если корней много, то самые близкие к мнимой оси корни называются доминирующими.

6.2.2. Оценка качества по частотным характеристикам.

 Частотные методы исследования САУ широко используют в инженерной практике. Они основаны на привычном для инженеров графическом изображении динамических характеристик систем, поэтому нашли применение при расчетах систем автоматического регулирования.

Передаточная функция замкнутой системы связана с ЧХ. Можно ввести понятия, которые определяют качества системы

  

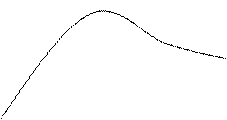
Типовой вид АЧХ замкнутой системы имеет вид:

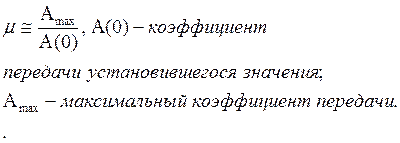
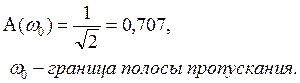
 - сигнал будет усиливаться

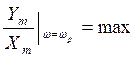
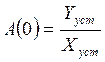
Сигналы, с частотами больше чем ω₀ не воспроизводятся.

Ширина полосы пропускания системы связана с быстродействием – интервал частот от 0 до , где

 - частота, на которой АЧХ  , на которой АЧХ уменьшается в  раз  (0,707=).

Считается, что система хорошо пропускает сигнал   и подавляет .

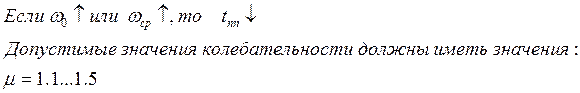
Оценки качества по ЛАЧХ разомкнутой системы.

Представим типовую ЛАЧХ, которая имеет вид:

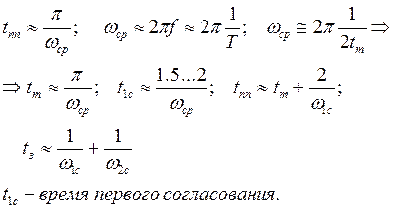
t_з – время запаздывания

Для перерегулирования справедлива следующая функция:

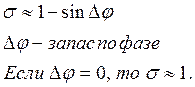
При затухании колебаний перерегулирование =t_m

Для практически устойчивых и работоспособных систем:

Теорема о связи ЛАЧХ и ЛФЧХ.

Если ЛАЧХ идет с наклоном n(-20дБ/дек) достаточно долго, то ЛФЧХ на этом же интервале частот стремится к n(-).

Интегральное звено .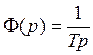

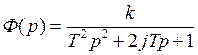
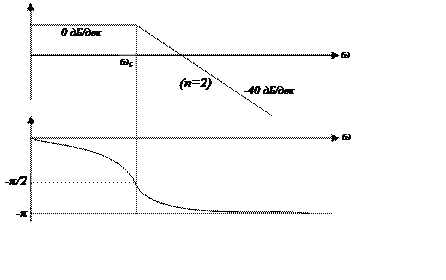
Вывод:

1. Если мы имеем экспериментально снятую ЛАЧХ, то мы можем сделать выводы о качестве системы без привлечения ЛФЧХ.

2. В области частоты среза желательно иметь минимальный наклон ЛАЧХ.

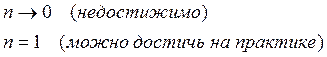
Для получения минимального перерегулирования нужно стремиться к минимальному наклону ЛАЧХ в области частоты среза.

6.2.3.Интегральные показатели качества.

Оценим качество 1-им числом, что особенно предпочтительно для аналитических исследований звеньев.

Будем оценивать по площади рассогласования.

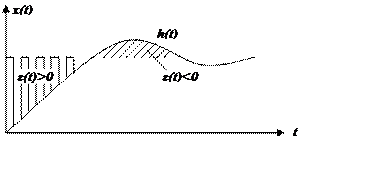
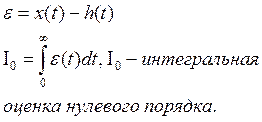
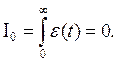
Система на грани устойчивости. Интегральная оценка несовершенна, т.к. не учитывает знакопеременный характер.

Наиболее удачной является интегрально квадратичная ошибка второго порядка.

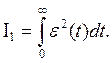
Может использоваться для аналитического проектирования.

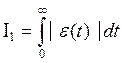
Интегральная оценка первого порядка.

–менее распространена в качестве системы.

Оптимизация удается только численным методом.

Существуют интегральные квадратичные оценки более высокого порядка (они связаны не со степенью, а с введением производных).

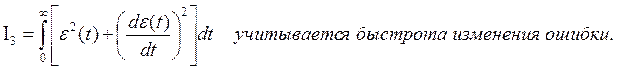
Показатели качества (разомкнутой системы).

Чаще на практике мы используем ЛАЧХ разомкнутой системы.

Предположим, нам известна ЛАЧХ разомкнутой системы

x                                                                 x(t)                   -

-20дБ/дек – наклон низкочастотной части ЛАЧХ                                       СЧ – среднечастотные

=коэффициент передачи равен 1

- частота сркза

 - частота второго сопряжения

ЛАЧХ сопутствует ФЧХ

запас                              по фазе -180

Теперь АЧХ и ФЧХ свяжем с показателями системы

t

Пусть типовая переходная функция имеет вид:

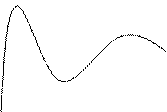
Важнейшим показателем является , который определяет быстродействие системы

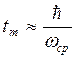
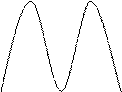
предположим, что сигнал резко колебательный

h     0     t             T/2

Полагаем, что  мы можем связать частоту среза с

Колебания системы обычно возникают на

               

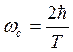
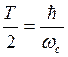
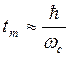
Следующая связь

  чем больше запас по фазе, тем больше

    

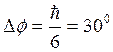
переригулирование составляет 50%

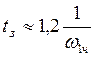 - формула не очень точная, но позволяет качественно оценить.