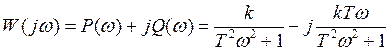
далее рассмотрения будут трафаретными
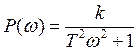 ;
; 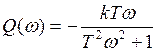
6) АЧХ
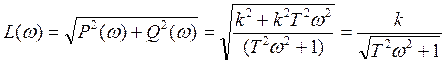
7) ФЧХ
![]() - аргумент
комплексного числа
- аргумент
комплексного числа
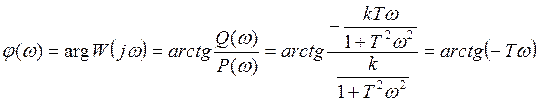
9) ЛАЧХ – асимптотические (предельные)
9.1рассмотрим низкочастотную ЛАЧХ
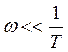 ,
, ![]()
обозначим 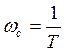 - частота сопряжения
- частота сопряжения
![]()
![]()
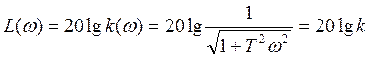
так как T<<1 ![]() можем пренебречь
этим слагаемым
можем пренебречь
этим слагаемым
9.2
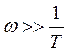 ,
, ![]()
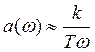
![]()
Полученные ЛАЧХ является асимптотическими, т.е. приближенными
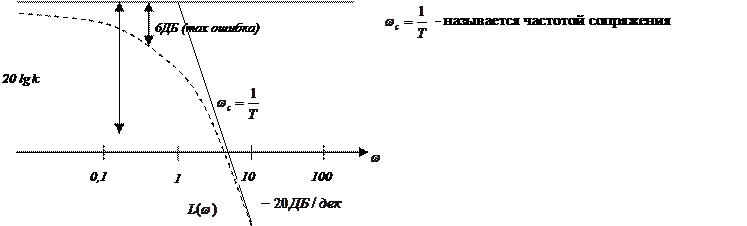 |
Высокочастотный совпал с низкочастотным,
дальше происходит уменьшение![]()
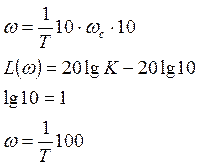
![]()
В инженерной практике пользуются асимптотическими прямыми.
Д.З. Оценить ошибку представления ЛАЧХ на частоте сопряжении.
9) АФЧХ
Самым простым способом объяснить, построив несколько точек
|
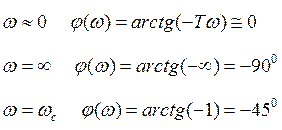
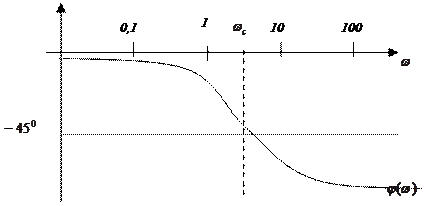 |
![]()
|
Изгибается центрально-симметрично относительно точки А.
10) Годограф АФЧХ
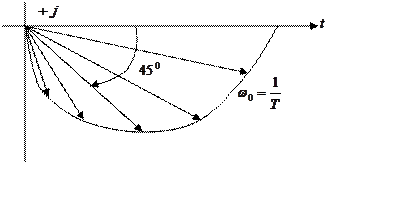 |
![]()
увеличивается в минус, поэтому поворачивается вниз; уменьшается по амплитуде
Д.З. Доказать годограф АЧХ полуокружности с диаметром k
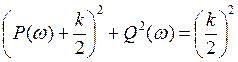
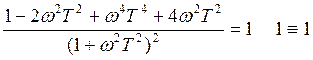
Практически важный свойства апериодического звена
10 Фильтр высоких частот
Апериодическое звено представляет собой фильтр пропускающий низкочастотные составляющие входного сигнала и ослабляющий высокочастотные компоненты
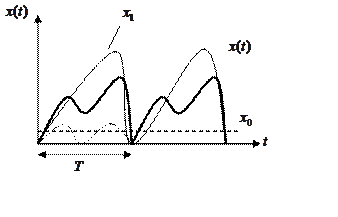 |
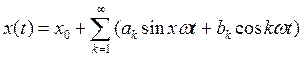
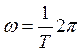 ;
; 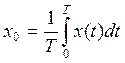
![]() ,
,![]() - амплитуда гармоничных составляющих
(образуют спиральный сигнал)
- амплитуда гармоничных составляющих
(образуют спиральный сигнал)
Любая периодичная функция может быть представлена суммой постоянных и гармонических составляющих.
![]() Образует спектр
функций
Образует спектр
функций
 |
Для не периодичной функции также можно сформулировать утверждение о разложении сигнала в спектр, в данном случае спектр будет не прерывным
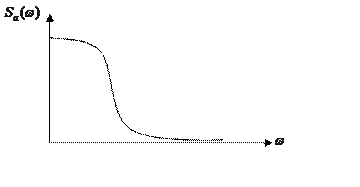 |
![]()
Частотная характеристика показывает как ослабляется или усиливается синусоидальный сигнал, проходящего через звено.
Таким образом частотная характеристика (в частности ЛАЧХ) показывает как деформируется спектр входного сигнала при преобразовании входного сигнала в выходной.
ЛАЧХ периодичного звена:
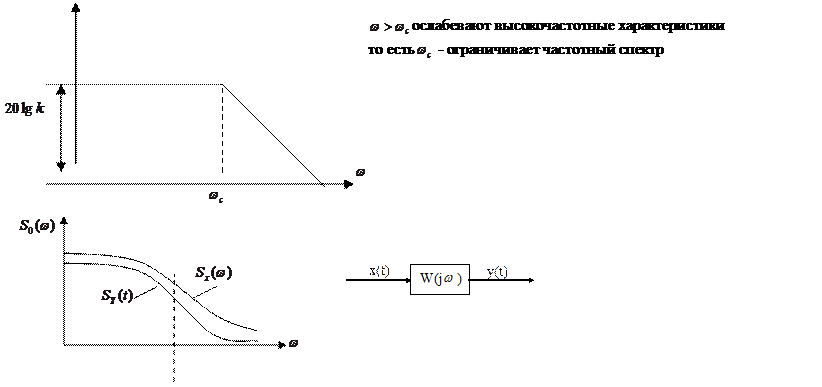 |
|||
|
|||
|
|
|||||
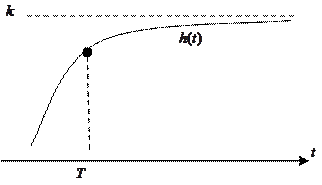 |
|||||
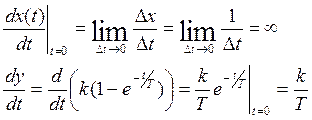
3.6 Дифференциальное звено
Дифференцирующим звеном называют звено, которое описывается уравнением y=kpu
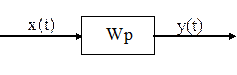 1)
Передаточная функция
1)
Передаточная функция
![]()
2) Дифференциальное уравнение
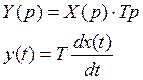
чисто дифференцирующих звеньев не существует, есть звенья, которые выполняют приближенное дифференцирование.
3) Переходная функция
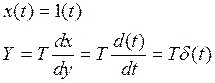
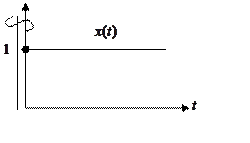 |
Рассмотрим пример:
Пусть используется датчик скорости, тахогенератор (позволяет получить обратную связь по быстроте перемещения)
Дифференциальное звено реагирует на быстроту изменения входного сигнала
 |
4) Весовая функция
|
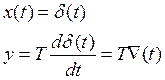
5) Частотная характеристика (Чх)
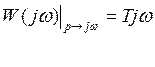
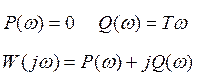
6) АЧХ
![]()
с ![]() коэффициент
передачи увеличивается (фильтр низких частот)
коэффициент
передачи увеличивается (фильтр низких частот)
7) ФЧХ
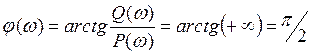 - получается
опережающий сигнал, который используется для компенсации запаздывания.
- получается
опережающий сигнал, который используется для компенсации запаздывания.
8) ЛАЧХ
![]()
![]() на 1, то
на 1, то ![]() на 20 ДБ
на 20 ДБ
![]() - прямая лини,
наклон +20ДБ на декаду и ось абсцисс пересекается в точке
- прямая лини,
наклон +20ДБ на декаду и ось абсцисс пересекается в точке ![]() , (так как увеличение х на 1 – это
возрастание в 10 раз) это следует из
, (так как увеличение х на 1 – это
возрастание в 10 раз) это следует из ![]()
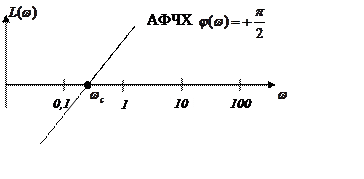 |
|||
|
|||
![]() - частота среза,
т.е.
- частота среза,
т.е. ![]() = 0, т.е. звено перестает усиливать
или ослаблять звено.
= 0, т.е. звено перестает усиливать
или ослаблять звено.
Диструкция связана с тем, что реальный сигнал имеет помехи. Спектр-помехи всегда существенно шире на меньшей амплитуде, чем у полезного сигнала. Дифференцирующее звено усиливает поехи тем сильнее, чем выше и частота. В результате соотношение сигнала дробь-шум ухудшается.
Пусть входной сигнал имеет вид:
На этот сигнал наложена помеха, она меньше по амплитуде, но более высокочастотная
![]()


![]()
![]()
![]()
![]()
Амплитуда любого выходного сигнала ограничена
![]()
![]() Y(t)
Y(t)
![]()
 |
![]()
![]() t
t![]()
![]() помеха будет усилена
помеха будет усилена
Из – за ограничения сигнала, мы его потеряем, если профилируем, то не узнаем полезного сигнала
9) АФЧХ
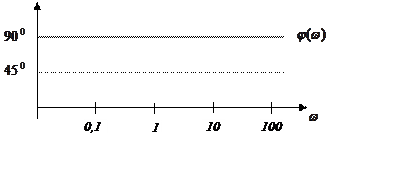 |
Дифференциальные звенья всегда увеличивают устойчивость системы
10) Годограф
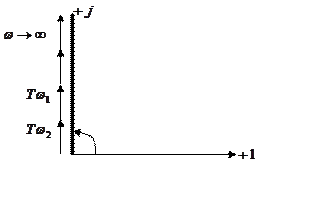
![]()
|
3.7 Форсирующее звено (звено первого порядка)
Форсирующим звеном первого порядка называют звено,
которое описывается уравнением ![]()
1) ![]()
порядок ![]()
![]()
![]()
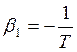
по теореме Безу количество корней совпадает с его порядком
![]()
отталкиваясь от передаточной функции, мы увидим, что за звено форсирует
2) ![]()
дает следующее уравнение во времени
![]()
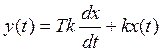
Сумма двух сигналов: производная сигнала и сам сигнал,
если 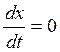
![]() ведет
себя как пропорциональное звено
ведет
себя как пропорциональное звено
![]()
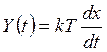
![]() - коэффициент
передачи установившегося значения
- коэффициент
передачи установившегося значения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.