Если
сравнивать эти процессы с биномиальным распределением, то время процесса
быстрее и имеется небольшое перерегулирование. 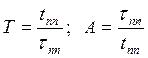 поэтому,
если нам известно задано время процесса
поэтому,
если нам известно задано время процесса ![]() ,
тогда мы можем задать
,
тогда мы можем задать 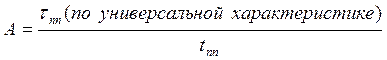
n=1 n=2 n=3
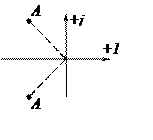 |
|||||
 |
|||||
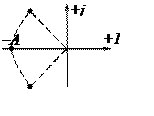 |
|||||
Сказанное позволяет перейти к примерам
7.2.5.Пример синтеза регулятора аналитическим методом.
Пусть объект задан передаточной функцией

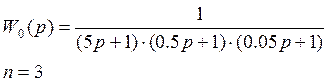
При последовательно включенных звеньев.
Требуется настроить систему на технический (модульный) оптимум.
Форма переходной кривой.
Время максимума tm = 1,5с.
Выбирая желанную форму переходного процесса для n=3
 1)
базовая постоянная времени:
1)
базовая постоянная времени:
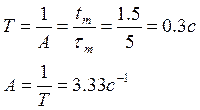
2) желаемая передаточная функция замкнутой системы:
Фжел(p) =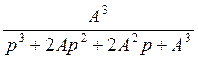 =
=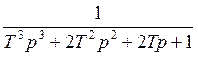
Передаточная функция разомкнутой системы:
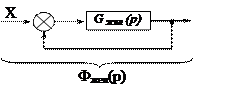 Gжел (р) =
Gжел (р) = 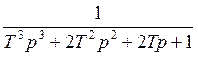
Фжел(p) = 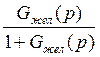 =
= 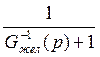
Выделение интегратора в разомкнутой системе свидетельствует об астатизме I поряка.
Gжел (р) = 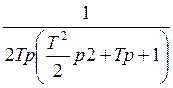
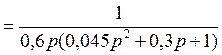
3) передаточная функция регулятора (корректирующее устройство).
Известно,
что ![]() :
:
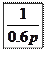
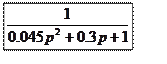
![]()
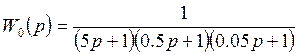
![]()
![]() - основное уравнение синтеза
- основное уравнение синтеза
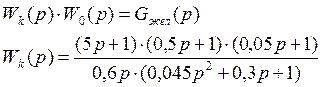
Если сделать такой регулятор, то замкнутая система удовлетворит требованиям.
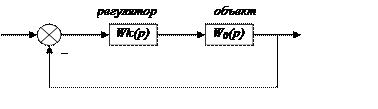
Реализовать такую систему не удается из-за высокого порядка.
Регулятор получается сложный. Для упрощения желательно использовать более простые объекты управления и желаемую передаточную функцию более низкого порядка. Это можно сделать, если синтезировать систему как многоконтурную, включая а контур лишь часть объекта.
7.2.6. Пример аналитического синтеза многоконтурной системы.
Поскольку сложность регулятора обусловлена объектом, то нужно разбить синтез на несколько этапов. На каждом этапе включать в передаточную функцию только простой объект. Это можно сделать, если система будет многоконтурной.
Будем считать, что звенья объекта расположены в следующем порядке:
|
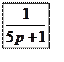
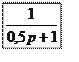
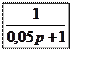
![]()
![]()
![]()
![]()
Будем
считать ![]() - сигналы датчиков промежуточного
регулирования величин. По каждому регулированию величины введем корректирующее
устройство и свою обратную связь.
- сигналы датчиков промежуточного
регулирования величин. По каждому регулированию величины введем корректирующее
устройство и свою обратную связь.
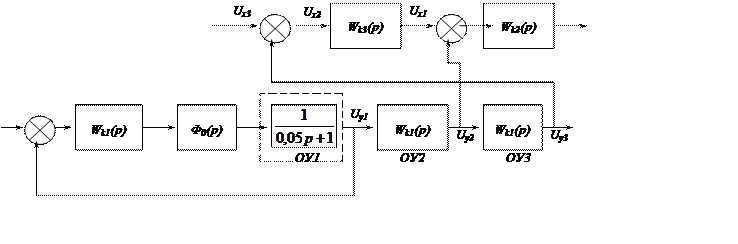
Объект управления представлен в виде последовательности трех звеньев.
![]() - дополнительное апериодическое
звено, которое имеет передаточную функцию следующего вида:
- дополнительное апериодическое
звено, которое имеет передаточную функцию следующего вида: 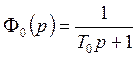
Произведена
декомпозиция (разбиение) объектов управления и организовано 3 контура низкого
порядка. Регуляторы Wk1(р) – Wk3(р)
получаются простыми (типа ПИ - регулятора). Каждый внутренний контур
оказывается подчиненным внешнему контуру, т.к. задание выработанного регулятора
внешнего контура. Такая система получила название системы подчиненного
регулирования. Используем для каждого контура настройку на модульный
оптимум (распределение по Батерворту). Предварительный вводимый фильтр 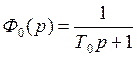 играет роль
ограничителя быстродействия системы, а постоянная Т0 называется некомпенсируемой
постоянной.
играет роль
ограничителя быстродействия системы, а постоянная Т0 называется некомпенсируемой
постоянной.
Первый контур:
Порядок контур должен быть не ниже второго, так как ввели дополнительное звено, возьмем n=2
![]() при распределении корней по
Батерворду будет выглядеть следующим образом
при распределении корней по
Батерворду будет выглядеть следующим образом
Фжел(p)= 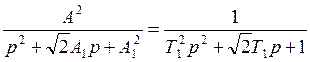 ,
,
где: А1 – среднегеометрический корень первого контура;
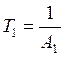 - базовая
постоянная времени.
- базовая
постоянная времени.
![]() - пока неизвестна, она определяется
на заключительном этапе
- пока неизвестна, она определяется
на заключительном этапе
Передаточная функция разомкнутого 1 контура:
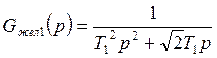
![]()
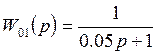
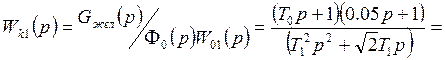
![]() -дополнительная постоянная, целесообразно выбрать
-дополнительная постоянная, целесообразно выбрать 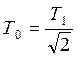 , чтобы упростить дробь; тогда
выразим
, чтобы упростить дробь; тогда
выразим ![]() через
через ![]()
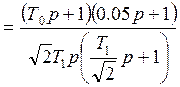
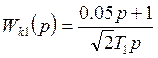

-
пропорциональ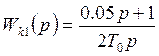 но - интегральный регулятор
но - интегральный регулятор
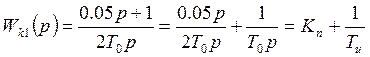
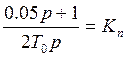 - передаточная функция
пропорционального звена
- передаточная функция
пропорционального звена
![]() - передаточная функция
интегрирующего звена
- передаточная функция
интегрирующего звена
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
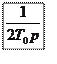
![]()
![]()
![]()
![]()
![]()
наиболее простой и наиболее реализуемый
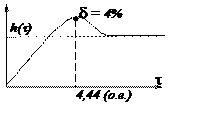
|



![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Выберем желаемую передаточную функцию второго контура, исходя из распределения корней по Батерворду. Выберем из таблицы функцию с порядком не менее 3 (порядок звена равен 1 + порядок первого контура, равно 1).
n=3
Фжел.2(p) =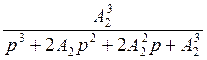 =
=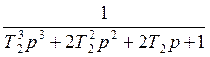
где: А2 – среднегеометрический корень второго контура
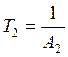
если мы выберем такую функцию, то желаемая функция разомкнутой системы будет иметь вид:
Gжел.2(р) =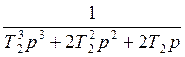 =
=
Вынесем
![]() за скобку и будем преобразовывать
так, чтобы функция походила на функцию 1 контура
за скобку и будем преобразовывать
так, чтобы функция походила на функцию 1 контура
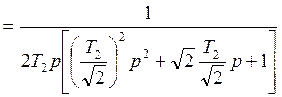
Потребуем
![]()
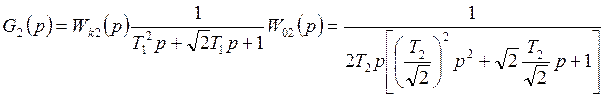
чтобы
правая и левая части совпали, нужно принять ![]()
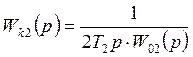
корректирующее
устройство должно компенсировать инерционность 2 подобъекта. Регулятор ![]() вносит интегратор во второй контур
с постоянной
вносит интегратор во второй контур
с постоянной ![]() . Это необходимо для обеспечения
заданного порядка астатизма, а постоянная
. Это необходимо для обеспечения
заданного порядка астатизма, а постоянная ![]() ,
связанная с
,
связанная с ![]() обеспечивает настройку второго
контура на модульный оптимум:
обеспечивает настройку второго
контура на модульный оптимум: ![]()
получим передаточную функцию второго контура в явном виде
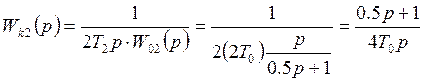
мы видим, что регулятор второго контура получается пропорциональным интегратором
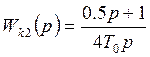
Форсирующая часть регулятора компенсирует второй контур. Проследим:
|
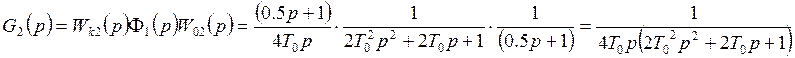 Третий контур:
Третий контур:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Порядок должен быть не ниже 4, т.к. подчиненный третий контур имеет третий порядок.
n = 4
Фжел.3(p) =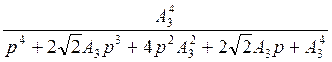
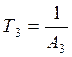
Фжел.3(p) =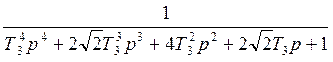
![]()
Gжел.2(р) =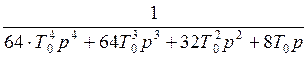 =
=
=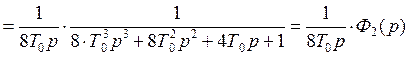
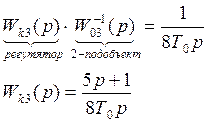
Расчет регулятора
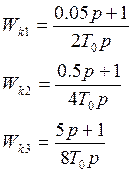
Определить
![]() некомпенсирующую постоянную
зависимость из условия требуемого быстродействия системы.(n=4)
некомпенсирующую постоянную
зависимость из условия требуемого быстродействия системы.(n=4)
![]()
![]()

![]()
![]()
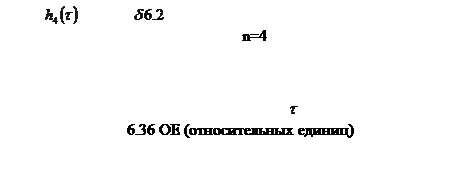
tmax = ? (время быстродействия)
tmax = 6,36
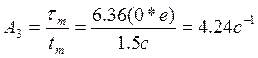
![]() вычислено для обеспечения реального
вычислено для обеспечения реального
![]()
Мы определили базовую постоянную для системы в целом

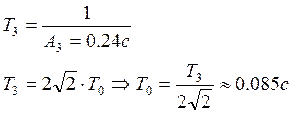
![]() задает масштаб, в прочесе,
зафиксированном в универсальной кривой
задает масштаб, в прочесе,
зафиксированном в универсальной кривой ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.