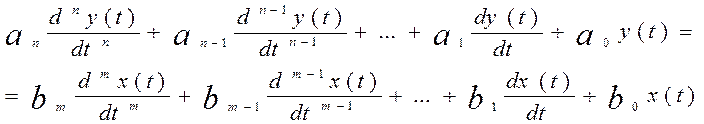Основы теории автоматического управления. Основные термины и определения, страница 3

 

(*)

Рассмотрим пример  математического очищения элементов САУ.

Допустим, мы имеем дело с механическим редуктором                            

                                         Редуктора имеет разное число зубьев  и                                  

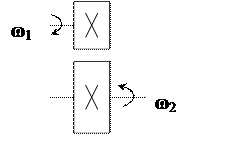                                       и вращаются с разной скоростью ω₁ и ω₂

                                   ω₁(t)    ω₂(t).

                                       связана с . В зоне контакта линейные скорости   

                                             равны:               

                                                                   

                                                     

                                                                                     Это уравнение можно                                                                         

                                                                                     преобразовать к    

                                                                                     уравнению (*), если , ,  и т.д. равны 0, то мы получим        .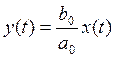

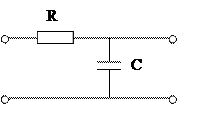
Рассмотрим следующую электрическую цепь

Uвых=Y(t)

ic

 

                                                                          

Uвх=X(t)

                                                                              

                                                
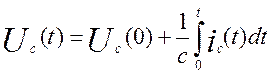
Эти 2 уравнения, описывающие процессы в цепи могут быть положены в основу уравнения (*). Сделаем преобразования
 

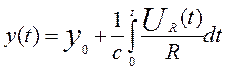
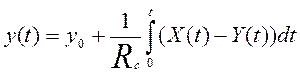
чтобы придать уравнению вид (*) нужно избавиться от интеграла, т.е. продифференцировать

  

                                                              

 

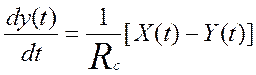
a₁=Rc

a₀=1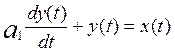              

₀=1         

Это уравнение описывает инерционное звено первого порядка

(апериодическое)                         

Предположим, входной сигнал скачкообразный

                                                                                                                   

                     

                      g                     U(t)

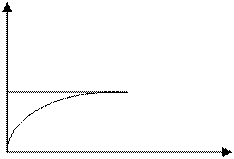
Если мы подадим на вход единичный ступенчатый  сигнал, то выходной сигнал будет вычисляться как ступенчатый. Мы как бы вбросим заряд, что приведет к напряжению на конденсаторе за очень маленький промежуток времени, поэтому процесс зарядки происходит мгновенно.

           U(t)

                                     Входной сигнал

                                                         t

    x, y  Y                            

x(t)

                                             выходной   

                                            сигнал

y(t)

                                                 

                                                    t

U(0)

Линейными называются звенья, обладающие следующим свойством:

Пусть реакция на сигнал X₁(t) выглядит, как Y₁(t), а сигналу X₂ соответствует

сигнал Y₂

X=X₁(t)       Y=Y₁(t)

X=X₂(t)       Y=Y₂(t)

Тоже для суммарного сигнала

X=X₁(t)+X₂(t) может быть найдена, как Y=Y₁(t)+Y₂(t)

                               Докажем, что звено (редуктор) является линейным:

                                X₁=2                       Y₁=4                       

                                X₂=3                       Y₂=6

                                X₃=X₁+X₂ =5         Y₃=Y₁+Y₂ =10

Можно показать, что звенья, описываемые уравнением (*) обладают свойством линейности, если коэффициент a₁,…,a_n=const и  b₁,….,b_n =const

2.2 Типовые сигналы систем автоматического управления.

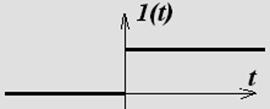
 а.  Единичный ступенчатый сигнал                                                                              

      Назовем единичным ступенчатым сигналом сигнал вида:

X(t)=1(t)=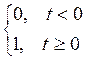

Физически это сигнал замыкающего контакта (релейный сигнал)  

Это функция называется функцией Хевисайда.

б. Импульсная дельта функция (функция Дирака)

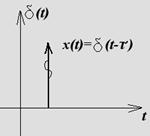
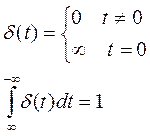
 называется предел последовательности прямоугольных импульсов, которые строятся по следующему правилу:

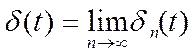
Дадим другое определение d - функции, как пределу последовательности приближений.

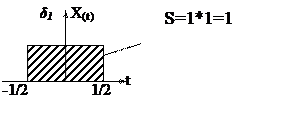Первое приближение.                                

δ ₁=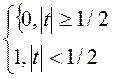

Второе приближение.                                                                

 δ ₂=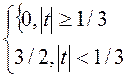                                                                       

Приближение  п - порядка

δ _n=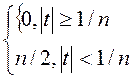

Площадь графиков каждого приближения постоянна и равна 1.

Свойства линейности

   Линейными называются звенья, обладающие следующими свойствами:

             Итак, пусть  выглядит , а сигналу  соответствует , тогда  может быть найдена .

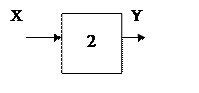                                            Докажем, что это звено линейное

                                             Звено передает сигнал с коэффициентом 2.

                                                     

                                             =5        =10

Все уравнения (*) будут линейными, если  и т.д. будут постоянными.

Д,З: покажите, пользуясь линейностью дифференцирования, справедливость этого утверждения.

в. Линейно изменяющийся сигнал

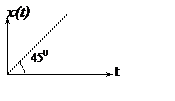X(t=)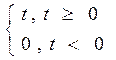

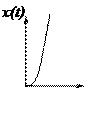г. Параболический сигнал

x(t)=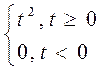

д. Гармонический(синусоидальный сигнал) сигнал

 

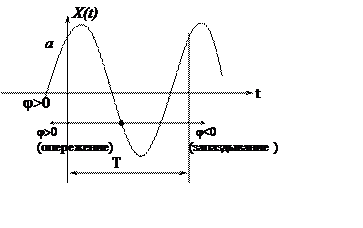Описывает соотношение:

X(t)=asin(wt+j)

          a-амплитуда

          j- начальная фаза (если начало синусоиды

         находится слева от оси X , то  будет со

         знаком “+”, если справа – со знаком  “-“)