Если гироприборы будут находиться в точке 2, то знаки в уравнениях для угла поворота руля и подъёмной силы руля поменяются на противоположные, и с точки зрения возврата x1 к xп добавка к подъёмной силе руля будет играть негативную роль, но с точки зрения прогиба эта добавка способствует разгибанию ЛА. При расположении гироприборов в хвостовой части ЛА по упругим колебаниям через систему угловой стабилизации реализуется жёсткая обратная связь. Упругие колебания будут затухать, поэтому гироприборы необходимо ставить в хвостовой части. Но по первому тону в точке 2 действительно существует устойчивый тон упругих колебаний, в то время как в точке 1 неустойчивый, зато по другим тонам мы можем получить картину обратную. Кроме того, нам придётся иметь гироприборы на каждой ступени ракеты или потребуется их лифтирование. Это в ряде случаев неприемлемо, поэтому, как правило, гироприборы устанавливают в носовой части, но приходится принимать меры по подавлению упругих колебаний. Можно ставить фильтры подавления упругих колебаний. Обычно это узкополосные самонастраивающиеся фильтры, тогда мы разрываем обратную связь по упругим колебаниям, и они затухают сами по себе за счёт диссипативных сил (потеря энергии в конструкции). Если колебания гаснут за счёт диссипативных сил, то такой способ называется пассивным. Активным называют способ, когда в гашении колебаний участвуют рули.
Если в диапазоне частот упругих колебаний инвертировать знак DJ, тогда и добавка DY тоже получится с минусом. Инвертирование знака у DJ равносильно переносу гироприборов из точки 1 в точку 2. Другой способ реализуется на основе сдвига фаз
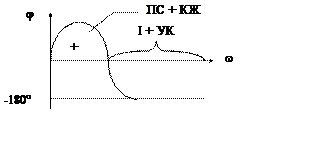 |
Это фазовое подавление упругих колебаний (здесь уже участвуют рули).
Сложность в том, что должен иметь место большой излом в фазочастотной характеристике корректирующего звена.
2. Требование к помехоустойчивости СУ полетом ЛА
Помехоустойчивость системы, способность системы выполнять свои функции при наличии помех. П. оценивают интенсивностью помех, при которых нарушение функций системы ещё не превышает допустимых пределов. Чем сильнее помеха, при которой система остаётся работоспособной, тем выше её П. Многообразие устройств и решаемых ими задач, с одной стороны, и видов помех — с другой приводят к необходимости специализированного подхода при рассмотрении П. в каждом конкретном случае. Требования к П. различных систем отличаются большим разнообразием: так, в радиолокационных системах иногда считают допустимым пропуск отдельных радиолокационных сигналов станцией (за время однократного обзора контролируемой ею области пространства), подлежащих обнаружению, а в системах передачи данных, использующих ЭВМ, часто недопустима потеря даже одного передаваемого знака из чрезвычайно большого их числа.
Рассмотренные системы управления (линейные и нелинейные) формально позволяют обеспечить заданные показатели качества при изменении параметров объекта управления в любых конечных пределах. Этот эффект практически достигается за счет того, что полоса пропускания частот выбирается большой, так что все изменения параметров приводят к изменению характеристик высокочастотных колебаний, которые практически не проявляются в регулируемой координате. Формально, чем выше частота высокочастотных колебаний, тем менее они заметны в выходном сигнале и казалось бы полосу пропускания частот системы целесообразно выбирать как можно большей. В действительности любые из рассмотренных систем, во-первых, содержат элементы с нелинейной статической характеристикой (типа насыщение) и, во-вторых, они работают в условиях сравнительно интенсивных высокочастотных помех.
Это значит, что при большой частоте «быстрых» движений в системе и тем более, если они будут многократно усиливаться, могут привести к «забиванию» нелинейного элемента, т.е. система будет помехонезащищенной.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.