Это значит, что при большой частоте «быстрых» парциальных движений в системе и тем более, если они будут многократно усиливаться и могут привести к «забиванию» нелинейного элемента, т.е. система будет помехонезащищенной.
Отсюда следует очевидный вывод, что система должна удовлетворять заданным показателям качества при минимально возможной полосе пропускания и при этом на высоких частотах частотная характеристика не должна иметь резонансных всплесков.
Критерием помехозащищенности в указанных условиях будет значение дисперсии (или СКО) на выходе нелинейного элемента при выполнении требований на показатели качества.
СУС работают в условиях помех. Параметры помех заранее предсказать нельзя. Можно лишь предположить только их возможные диапазоны. Однако, данные телеметрии показывают, что в сигнале помех всегда можно выделить гармонику, амплитуда которой превышает амплитуды других гармоник. Это позволяет упростить задачу отыскания помехоустойчивости системы.
Под помехоустойчивостью понимают работоспособность системы в условиях помех. Будем считать, что на входе системы помимо полезного сигнала действует гармоническая помеха:
![]()
При этом частота помехи хотя бы на порядок выше максимальной частоты полезного сигнала. Помехи такого рода по месту их возникновения делятся на:
· Внешние (вызывающие вынужденные колебания в системе).
· Внутренние (возникающие в замкнутом контуре системы как автоколебания и определяются свойствами самой системы).
Примеры внешних помех:
· Помехи возникающие из-за автоколебательного режима измерительных устройств;
· Автоколебания, возникающие в общих цепях питания различных элементов и блоков СУ;
· Ступенчатость характеристик потенциометрических датчиков или задания программ.
Внешние помехи в основном представляют собой гармонические составляющие сигналов управления, возникающие в результате автоколебаний на частотах упругих колебаний и колебаний жидкости. Эти помехи приводят к возникновению нелинейности, т.е. в условиях помех меняются коэффициенты передач нелинейных звеньев по полезному сигналу.
С помехами можно бороться двояко:
Ликвидировать источники помех.
Для внутренних помех - выбор параметров системы таким образом, чтобы в ней не появились автоколебания с недопустимыми параметрами, при которых система по полезному сигналу стала бы неустойчива. Т.к. Вп и Wп заранее неизвестны, то в общем случае в результате исследования помехоустойчивости необходимо определить область значений параметров помехи, при которых система устойчива по полезному сигналу.
Если Вп и Wп лежат в заштрихованной области, то они не сильно размывают существующие нелинейности и это не приводит к изменению по полезному сигналу.
Кривая, ограничивающая область параметров помехи, при которых система устойчива называется кривой помехоустойчивости: Вп=f(Wп).
Если параметры лежат на кривой помехоустойчивости, то система находится на границе устойчивости.
Заметим, что для линейных систем рассмотренное понятие помехоустойчивости не имеет смысла. В них действует принцип суперпозиций и наличие помех не вызывает потери устойчивости.
Для нелинейных систем не действует принцип суперпозиций.
|
|
Рассмотрим физическую картину прохождения сложного сигнала через нелинейное звено. Нелинейных звеньев в СУС много, поэтому придется рассматривать только основную нелинейную характеристику СУС.
В качестве такой основной характеристики в СУС выступает скоростная характеристика рулевой машинки.
Статическая характеристика имеет вид:
2. Рулевой привод как объект регулирования и элемент СУ.
Рулевой привод – усилитель, рулевая машинка и привод.
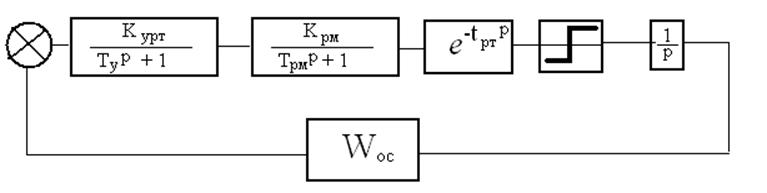
Варианты ОС
Wос = Кос – жесткая ос
Wос = Тоср+1 – гибкая ос
Wос = 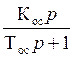 - непонятно
какая J (вероятнее всего имеется ввиду диф. с замедлением)
- непонятно
какая J (вероятнее всего имеется ввиду диф. с замедлением)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.