Ответы на экзаменационные билеты № 1-24 по дисциплине "Механика полета" (Типовые законы управления рулями ЛА. «Мгновенный» и «фактический» промах), страница 29

1.Каждому параметру должна соответствовать проверка

2.Родился из практики синтеза методом макетирования радиотехнических систем). Проверяется характер функционирования системы в целом на некоторых контрольных тестах. В этих ситуациях задается область некой совокупности контролируемых переменных. Если переменные выходят из области, то 2-а варианта: идет на доработку или расширяются допуска.

Можно контролировать много параметров, например, контролировать по переходному процессу.

Замена статистического исследования исследованием на детерминированных моделях как ускорение или удешевление синтеза: подход: детерминированный синтез с проверкой системы при изменении допусков:

-  степень статической неустойчивости ОУ

-  эффективность органов управления

-  передаточное число по угловой скорости

-  добротность РП и др.

Все допуска на все параметры разыгрываются. Есть 2-а метода приближения детерминированной постановки к стохастической:

1.  Метод критических реализаций

2.  Метод использования неоднозначной связи между случайными процессами и их спектральными плотностями.

1.По результатам статистического моделирования давно было сделано наблюдение: если в ходе проверки случается что-нибудь нежелательное, то это означает, что как минимум 2-а параметра вышли из ±2δ закона распределения. Исходный розыгрыш случайных параметров без моделирования может считаться приводящим к успеху без осуществления моделирования.

2. 

Sx(w)®форма импульсов

Билет 20.

1. Основное кинематическое тождество методов наведения.

Для того чтобы иметь возможность получения уравнений для различных методов наведения, выведем основное кинематическое тождество.

Будем считать цель и перехватчик материальными точками. Также будем пренебрегать переходными процессами и запаздываниями. Получающиеся при этом упрощения очевидны; «загрубления» позволяют проводить  содержательный и качественный анализ методов, сопоставлять эти методы друг с другом.

Пусть О – неподвижная точка. На рисунке 1 представлена схема взаимного расположения ракеты и цели.

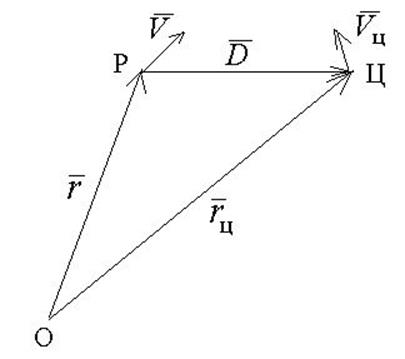
Рисунок 1 – Схема взаимного расположения ракеты (Р) и цели (Ц)

Введем единичный орт , то есть, , а . Из простых геометрических соображений

.

Продифференцируем левую и правую часть этого уравнения по времени, имеем

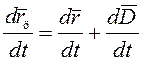.                                                            (1)

Так как точка О неподвижна, то производная есть абсолютная скорость ракеты

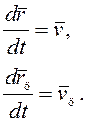
Абсолютная скорость цели

                                                  (2)

Производная орта(линии визирования) есть

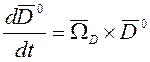, где - абсолютная скорость .

Подставим полученные соотношения в формулу (2):

.

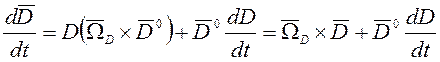Таким образом, основное кинематическое соотношение, исходя из формулы (1), можно записать в виде

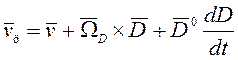.                                                     (3)

Запишем уравнение (3) в проекциях на оси системы координат xy. Одну из осей свяжем с линией ракета-цель.

, где - орт оси z, . Обозначим . Тогда , .

Имеем такую систему уравнений

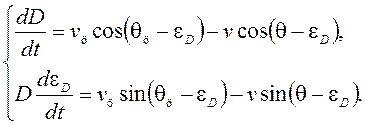                                 (4)

К этой системе уравнений для расчета траектории следует добавить уравнение метода наведения .  - заданы. Система (4) содержит переменные: .

Следует отметить, что при произвольном движении цели задача решается только методами численного интегрирования.

2. Режекторные фильтры.  

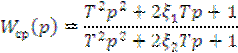
условия :

ξ₁<0,3

ξ₂>0,7

            Разновидность заграждающего (режекторного) фильтра; представляет собой включаемый в электрическую цепь двухполюсник (обычно параллельный колебательный контур), сопротивление которого резко увеличивается в некоторой относительно узкой полосе частот,  препятствует прохождению переменных токов в этой полосе частот и пропускает токи с частотами, лежащими за её пределами.

Обеспечивает отрицательный фазовый сдвиг:

Режекторный фильтр (фильтр-пробка) подавляет определенную частоту во входном сигнале. Он может быть спроектирован непосредственно по z-диаграмме.

Билет 21.

1.Кинематические соотношения метода погони.

Метод погони – метод наведения, при котором во все время движения вектор скорости ЛА направлен на цель (рисунок 1).