Ответы на экзаменационные билеты № 1-24 по дисциплине "Механика полета" (Типовые законы управления рулями ЛА. «Мгновенный» и «фактический» промах), страница 4

При данном методе вектор скорости ракеты V_p в каждый момент времени t направлен в точку упреждения, то есть точку, где произошла бы встреча цели и ракеты, если после момента времени t они двигались бы равномерно и прямолинейно . Рассмотрим ситуацию, представленную на рисунке:

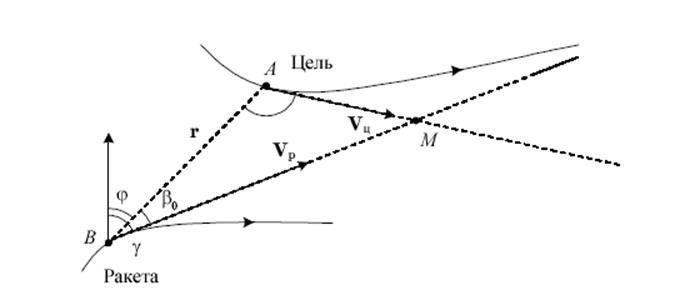
Здесь цель и ракета движутся по некоторым криволинейным траекториям и в момент времени t находятся, соответственно, в точках А и В. Точка упреждения М для момента времени t находиться как точка пересечения лучей, являющихся продолжением векторов скоростей цели V_ц и ракеты  V_р. Угол β_о можно определить из треугольника АВМ.

Угол β_о называется идеальным углом упреждения. В любой момент времени угол упреждения для метода параллельного сближения должен быть равен β_о.

При движении цели угол α, угол между вектором скорости цели V_ц и направлением  на ракету, постоянно меняется. Следовательно, будет меняться и угол β_о. Однако, как показывает анализ, вектор r, соединяющий точки расположения ракеты и цели, будет перемещаться в пространстве параллельно самому себе, не вращаясь. Это свойство определило название метода. Учитывая последнее обстоятельство, для метода параллельного сближения будет справедливо равенство:

По сравнению с методом погони метод параллельного сближения дает минимальную кривизну траектории движения ракеты.

Билет №3

1 Упрощенный метод оценки параметров автоколебаний в контурах угловой стабилизации.

В нелинейной автоколебательной САУ эффективный коэффициент усиления регулятора по медленной составляющей сигнала обратно пропорционален амплитуде автоколебаний, которая, в свою очередь, является некоторой функцией переменных параметров объекта управления. Причем если амплитуда автоколебаний при некоторых структурах САУ прямо пропорциональна коэффициенту усиления объекта, зависимость ее от других параметров объекта более сложна.

САУ технически работоспособна при амплитуде автоколебаний, не превышающей некоторое максимальное значение, поэтому пределы изменения переменных параметров объекта управления, при которых САУ сохраняет свою работоспособность, жестко ограничены. Их можно значительно расширить путем выбора рациональной структуры САУ.

Анализ и синтез таких систем удобно проводить на базе метода гармонической линеаризации.

Известно, при выполнении условия

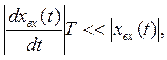
где  - внешнее воздействие; Т – период автоколебаний нелинейной САУ, процессы в некоторой нелинейной системе приближенно можно описать следующими уравнениями:

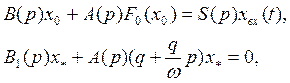
где  - функция смещения соответствующего для медленного меняющейся составляющей;  - медленно меняющаяся составляющая;  - высокочастотная колебательная составляющая.

Учитывая, что , как правило, является непрерывной плавной функцией, при малых значениях  ее можно линеаризовать, т.е.

Тогда уравнение для медленного меняющейся составляющей можно записать в виде  где  - эквивалентный коэффициент усиления нелинейного усилителя, т.е. по отношению к медленно меняющимся внешним воздействиям такая система ведет себя как линейная.

В связи с этим при медленно меняющихся воздействиях автоколебательную САУ можно заменить эквивалентной линейной.

Для пояснения:

Физическая картина работы системы угловой стабилизации на упругой ракете

Пусть программное положение x₁ следующее:

Но под действием возмущений продольная ось отклонилась от программного направления. Пусть гироприборы расположены в точке 1, тогда

.

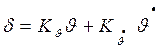J будет измерена гирогоризонтом и произойдёт отклонение руля на угол d. На руль действует подъёмная сила Y_p, создающая момент M_y, возвращающий КА к x_п. Но под действием Y_p происходит прогиб. Если гироприборы  находятся в точке 1, то они реагируют уже на J_г=J + DJ’.

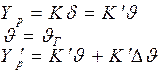
Возникнет увеличение подъёмной силы на руле.

Таким образом, при расположении гироприборов в носовой части ЛА через систему угловой стабилизации по упругим колебаниям реализуется положительная обратная связь. Она приводит к нарастанию амплитуды упругих колебаний. Амплитуда будет возрастать, пока в каком-то звене не сработает насыщение или ограничение. Тогда прекратится рост амплитуды и появятся автоколебания на частотах упругих автоколебаний.