Ответы на экзаменационные билеты № 1-24 по дисциплине "Механика полета" (Типовые законы управления рулями ЛА. «Мгновенный» и «фактический» промах), страница 18

Отметим, что положение экстремалей довольно устойчиво по отношению к вариациям тяги и лобового сопротивления, хотя величина избытка тяги  на экстремали при этом существенно изменяется.

См. билет 13(2)

2. Комплекс САУ ЛА. Состав и назначение систем комплексов.

Система управления летательным аппаратом – комплекс приборов, устройств, агрегатов, предназначенных для контроля состояния, поддержания боевой готовности, подготовки, пуска и управления полетом БР с целью поражения объектов противника с заданной эффективностью.

В состав системы управления включаются следующие приборы, устройства и агрегаты:

·  комплекс командно-измерительных приборов ИНС;

·  БЦВК;

·  комплекс преобразующей, коммутационной и распределительной аппаратуры;

·  устройства ввода и хранения данных полетного задания на пуск;

·  бортовые источники электропитания СУ;

·  силовые приводы с необходимыми источниками энергии, предназначенные для приведения в действие органов управления ракетой;

·  исполнительные устройства электро-, пневмо- и пироавтоматики;

·  бортовая кабельная сеть.

Таким образом, в соответствии с данным определением, СУ представляет собой одну из функциональных подсистем более сложного технического объекта, каким является сам ЛА,  и находится в одном ряду с другими функциональными подсистемами БР, к числу которых относят двигательные установки с собственной автоматикой регулирования режимов их работы, систему автоматики боевых блоков, систему телеизмерений с соответствующей регистрирующей и радиопередающей аппаратурой.

Билет №13

1. Реализация оптимальной программы набора высоты и скорости для ЛА, совершающего полет в атмосфере.

Основные допущения:

поле потенциальной силы тяжести – плоское полная энергия массы ЛА :

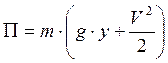
Полная энергия отнесенная к единицы массы ЛА:

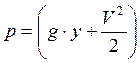
Относительным изменением массы ЛА в процессе перехода на новый режим полета можно пренебрегать

Избыток тяги над лобовым сопротивлением и расход горючего зависят только от высоты

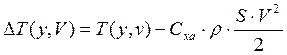
и скорости полета:

Допущение о локальной гладкости функций, позволяющее использовать для поиска экстремалей уравнение Эйлера.

Две постановки задачи локальной оптимизации барограммы набора высоты y(V)

В первой постановке следует минимизировать время маневра:

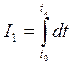
Во второй постановке минимизируется расход горючего:

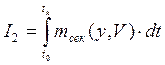
С конечной целью представить функционалы качества в виде интегралов по скорости полета сделаем промежуточный шаг и представим их в виде:

       

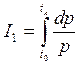
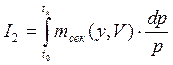
Используем допущение о монотонности нарастания скорости полета, произведем еще одну замену переменной интегрирования. Воспользуемся соотношениями:

    

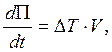
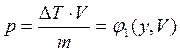
Из 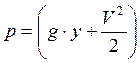 следует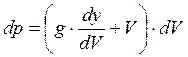

Приходим к выражениям для минимизируемых функционалов:

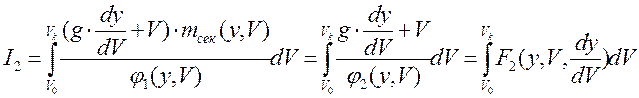
Здесь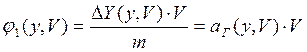

- ускорение в горизонтальном полете

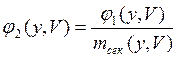
Обе постановки приводят к задаче поиска экстремума функционала вида:

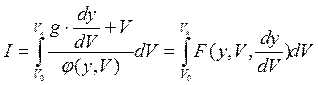
Решение

Искомые экстремали y(V) должны удовлетворять уравнению Эйлера относительно подынтегральных функций:

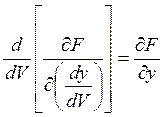              где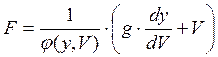

Раскрыв обе части уравнения и приводя подобные члены, сокращая на нулевой общий множитель, имеем: 

       или              (*)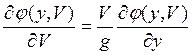

В первой постановке из уравнения (*) следует:

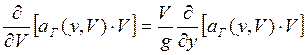  либо(m=const):

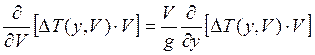
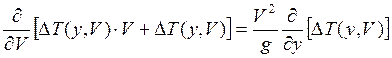
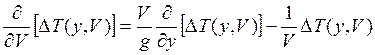 или

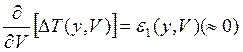
Величина в правой части полученного уравнения меняется плавно и мала, т е мы получаем условие близкое к условию локального, для данной высоты, максимума скорости нарастания полной энергии.

Фиксируя высоту полета y, получаем точку экстремали (y,V).

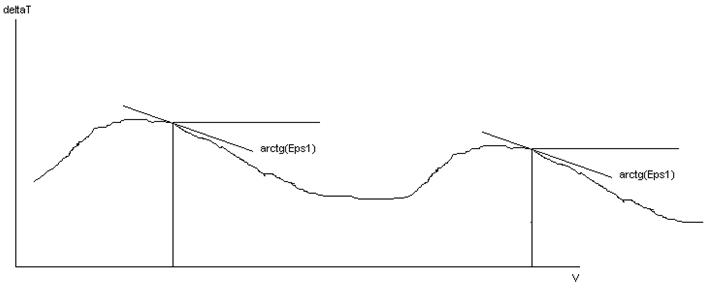
Во второй постановке получаем несколько более сложное выражение:

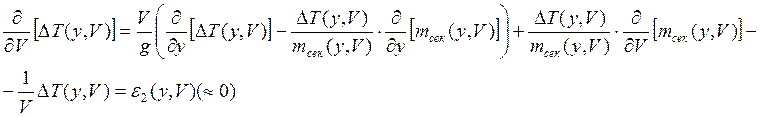
И в этом случае величина в правой части невелика и меняется плавно, что облегчает вычисления, очень сходные по процедуре и по результатам с теми, что имеют место при первой постановке задачи.

С ростом скорости   растет быстрее чем , поэтому при этом и сближаются. Это практически снижает вопрос о выборе критерия оптимизации и позволяет ограничиться решением задачи во второй постановке: по минимуму расхода горючего.