Ответы на экзаменационные билеты № 1-24 по дисциплине "Механика полета" (Типовые законы управления рулями ЛА. «Мгновенный» и «фактический» промах), страница 2

Пусть компоновка ЛА статически устойчива, тогда  берётся с плюсом. Если же компоновка статически неустойчива, тогда  с минусом, и звено будет неустойчивым, но зато и  с минусом, и обратная связь станет отрицательной, то есть будет способствовать устойчивости. Но неустойчивость звена сказывается сильнее, чем отрицательная обратная связь. Таким образом, в любом случае движение ЛА неустойчиво, и требуется система управления.

Чем же можно пренебречь при приближённых исследованиях. Допустимые упрощения показаны на рис.

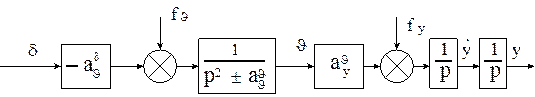
То есть угловое движение можно рассматривать без учёта движения центра масс, но наоборот нельзя.

Параметры движения центра масс  с угловыми параметрами J связаны интегральными зависимостями. АЧХ интегрирующих звеньев падающие. Это указывает на то, что движение центра масс более низкочастотное, чем угловое движение. Сейчас частоты управляемого углового движения порядка 0,01¸1 Гц, а частоты управляемого движения центра масс на порядок меньше.

Билет №2

1. Методы оценки показателей устойчивости контуров управления перегрузкой и угловой стабилизацией. Рекомендации по заданию их целевых значений.

Под устойчивостью понимают способность системы самостоятельно приходить к последующему установившемуся состоянию после приложения воздействия, которое вывело её из состояния равновесия. Исследование устойчивости является одной из основных задач в теории автоматического управления.

Замкнутая цепь в силу свойств, обусловленных наличием обратной связи, склонна к неустойчивой работе. В процессе регулирования сигнал с выхода передается на вход группы звеньев системы, среди которых могут быть многоёмкостные (колебательные элементы). Приложение внешнего воздействия может привести к возмущенному состоянию системы, сопровождающемуся колебаниями регулируемой (выходной) величины. Наличие главной обратной связи будет способствовать поддержанию колебательного процесса и при больших коэффициентах усиления, если параметры системы не обеспечивают необходимого затухания (рассеивания) энергии колебаний, может привести к неустойчивой работе, характеризуемой неограниченным возрастанием амплитуды колебаний.

Работа САУ в переходном режиме описывается системой дифференциальных уравнений, на основании которых может быть написано одно-единственное дифференциальное уравнение. Его порядок определяется количеством и свойствами динамических звеньев.

При исследовании устойчивости САУ возможно решение следующих задач:

-  выяснение, является ли устойчивой система при заданных параметрах;

-  определение допустимых изменений некоторых параметров (при неизменных остальных параметрах и заданной структуре) без нарушения устойчивости системы;

-  анализ структуры системы и определение параметров, при которых она может стать устойчивой (анализ структурной устойчивости).

В большинстве практических случаев устойчивость не является достаточным условием нормального функционирования системы автоматического управления. В зависимости от заданного технологического режима САУ должна обеспечивать требуемое качество работы установки в переходных режимах, вызванных изменением задающего, либо возмущающего воздействия. Качество регулирования принято оценивать следующими основными показателями: время регулирования, перерегулирование, колебательность системы, частота колебаний переходного процесса.

Исследуемая система неустойчивая, поэтому изменяем параметры элементов СУ, вводя дополнительные корректирующие элементы, добиваемся желаемого результата (устойчивости системы или требуемых показателей качества), оптимизируя закон регулирования или параметры регулятора. Увеличивая коэффициент усиления, получили желаемый результат.

Согласно критерию Найквиста, чем дальше АФЧХ от критической точки     (-1, j0), тем больше запас устойчивости. Различают запасы устойчивости по амплитуде и по фазе.

Устойчивость СУ можно количественно оценить запасом устойчивости по фазе и амплитуде (усилению):