Ответы на экзаменационные билеты № 1-24 по дисциплине "Механика полета" (Типовые законы управления рулями ЛА. «Мгновенный» и «фактический» промах), страница 20

 (этот момент заставляет ЛА поворачиваться на угол атаки )

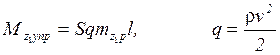
S – характерная площадь, l – характерная длина

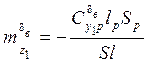
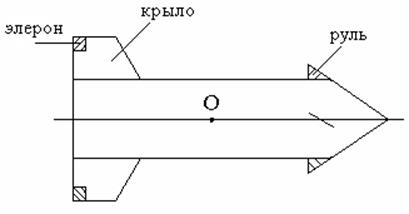
Воздушные рули в зависимости от назначения ракеты могут располагаться в различных частях её корпуса. У баллистических ракет воздушные рули располагаются на задних кромках неподвижных стабилизаторов. Ракета имеет 4 руля, оси вращения, которых лежат в плоскостях соответствующих стабилизаторов и перпендикулярны оси ракеты.

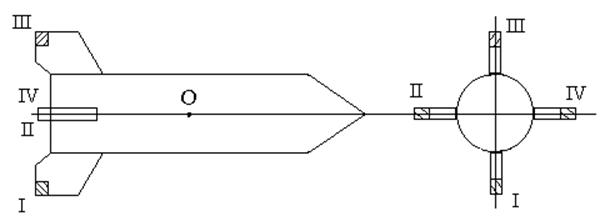
Рули II, IV называются рулями высоты. Они синхронно связаны друг с другом, т.е. имеют один привод. При их совместном отклонении от нейтрального положения возникает сила , которая  действует в вертикальной плоскости (крен стабилизирован) и управляет по углу тангажа.

Рули I, III расположены в вертикальной плоскости и используются для управления по углу рысканья  и по углу крена . Для управления по углу рысканья рули I, III должны поворачиваться в одном направлении, создавая потребную боковую управляющую силу . Для парирования крена рули I, III должны поворачиваться в разные стороны, создавая необходимый крутящий момент . Т.к. управления по углам  и  должно осуществляться непрерывно и одновременно, то рули I, III должны поворачиваться независимо друг от друга, для чего, в отличие от рулей II, IV, они имеют раздельные приводы.

У крылатых ракет, оперение и крылья которых используются не только для обеспечения статической устойчивости, но и для увеличения коэффициентов боковой и подъёмной сил C_y и C_z, рули по отношению к крыльям могут располагаться по 3 аэродинамическим схемам:

1) нормальная схема: рули позади крыльев и ц.м.;

2) «бесхвостка» (у противотанковых управляемых ракет и снарядов): рули позади ц.м., но не отдельно от крыльев, а на задних кромках крыльев;

3) «утка»: рули впереди крыльев и ц.м. .

1)

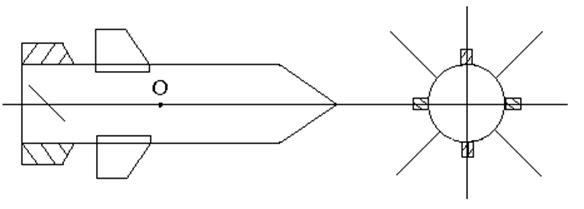
2)

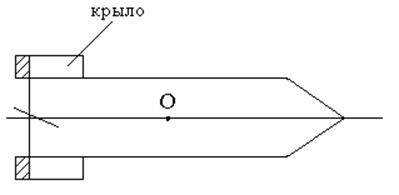
3)

Одно из описаний объекта управления – дифференциальные уравнения. Получают эти уравнения на основе составления уравнений моментов и сил. Причём уравнения моментов составляют относительно связанной системы координат, а уравнения сил составляют в скоростной системе координат. А затем с помощью матрицы управляющих косинусов переводят в программную систему координат.

В уравнениях моментов учитывают инерционные моменты М_ин, аэродинамические моменты М_аэр., демпфирующие М_демпф. (они пропорциональны угловой скорости w), возмущающие М_{возмущ.} и управляющие моменты М_упр. А в уравнениях сил учитывают инерционные, аэродинамические, демпфирующие, возмущающие, управляющие силы, а также силу тяжести. Уравнения получаются нелинейные, нестационарные и с перекрёстными связями, что неудобно при предварительных расчётах. Для упрощения уравнений пространственного движения осуществляют их линеаризацию. Линеаризация отстраивает от некоторых сложностей, но не избавляет от переменности коэффициентов. То есть нестационарность остаётся.

После линеаризации уравнения разбиваются на три группы:

уравнения продольного движения (в них присутствуют ), уравнения бокового движения (

уравнения касательного или тангенциального движения (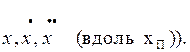

При этом удобно уравнения моментов записывать как уравнения угловых ускорений, а уравнения сил удобно записывать как уравнения линейных ускорений. Уравнения моментов делят на момент инерции ЛА, а уравнения сил делят на массу ЛА.

Пример.

     (1)

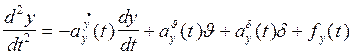                               (2)

.

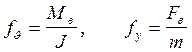Все коэффициенты имеют два индекса: нижний – к какому уравнению относится коэффициент, верхний – при какой переменной стоит этот коэффициент. Знаки этих коэффициентов учтены в самой форме записи. Если центровка или компоновка статически устойчива, берут верхний знак, а неустойчива – нижний. Все значения коэффициентов положительны, но должно быть примечание – какая компоновка. Обычно идут на разные ухищрения, чтобы компоновка была статически устойчива.

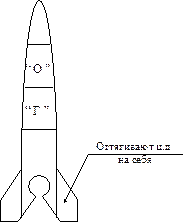
Охарактеризуем некоторые коэффициенты.

 – аэродинамический коэффициент, учитывающий влияние скорости движения центра масс на угловое движение ЛА (коэффициент аэродинамической обратной связи). Его проявление иллюстрируется на рис. 17. Этот коэффициент мал, оказывает малое влияние на динамику системы и при приближённых исследованиях им пренебрегают.