Решение получается в конечном виде. Для сверхзвукового ЛА – в виде семейства двух экстремалей на плоскости (V,y). Эти решения не содержат произвольных постоянных, которыми можно было бы воспользоваться, чтобы удовлетворить заданным граничным условиям. В общем случае экстремали в такой задаче могут вообще не проходить через заданные граничные точки.
Таким образом, рассматриваемая вариационная задача не имеет решения в классе непрерывно дифференцируемых функций.
Тем не менее, решение в классе кусочно-гладких функций находится.
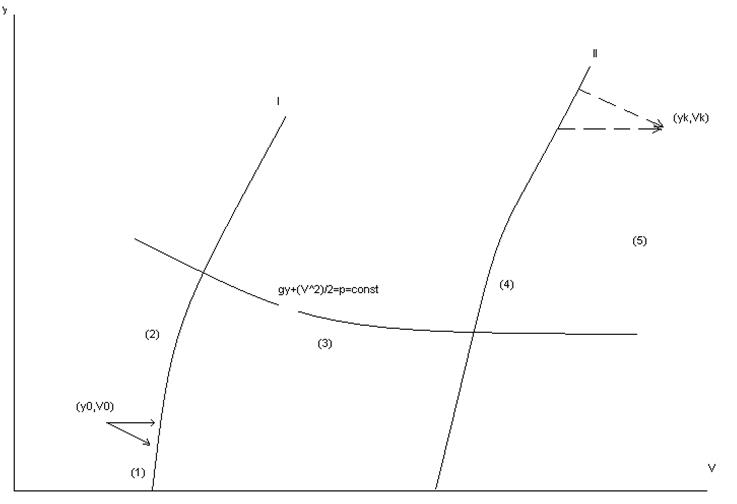
Первый участок (1)- скорейший выход на первую экстремаль ( I ).
При отсутствии запаса по высоте это – разгон до соответствующей скорости по горизонтали. При возможности “перекачки” потенциальной энергии высоты в кинетическую – разгон со снижением; предельный случай - мгновенный переход на экстремаль ( I ) за счет уменьшения высоты полета:
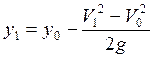
Второй участок (2)- набор высоты с небольшим увеличением скорости, которая остается дозвуковой, по экстремали ( I ).
На участке (3) – скорейший переход на сверхзвуковую экстремаль. Он может быть организован со снижением, в пределах – до
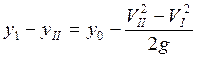
Если на высоте Yk конечная заданная скорость Vk больше, чем скорость, соответствующая экстремали II, может оказаться выгодным использовать такую возможность дальнейшего движения по экстремали II и последующего снижения с разгоном до скорости Vk. Обычно выбор Yk продиктован некоторыми ограничениями, поэтому в точке экстремали II, соответствующей несколько меньшей высоте, активизируется программа плавного перехода на маршевую высоту полета.
Отметим,
что положение экстремалей довольно устойчиво по отношению к вариациям тяги и
лобового сопротивления, хотя величина избытка тяги ![]() на экстремали при этом существенно
изменяется.
на экстремали при этом существенно
изменяется.
2. Тактико-технические требования, предъявляемые к СУ полетом.
Требования к системам управления.
В соответствии с РК-86, к системам управления предъявляются следующие требования:
1. Обеспечение управления с заданной точностью. Точность может задаваться статическими, динамическими, статистическими и суммарными ошибками.
|
|
2. Обеспечение заданных характеристик устойчивости (запасы устойчивости по фазе и по амплитуде). Степень устойчивости может определяться по расстоянию от мнимой оси до ближайшего корня, по положению рабочей точки в области устойчивости в параметрах Кj и Кi закона управления. Совокупность выбранных коэффициентов в системе называют рабочей точкой. Рабочую точку выбирают так, чтобы обеспечивались двойные запасы на изменение коэффициентов. Характеристики устойчивости косвенно характеризуют надёжность системы.
3. Обеспечение заданной надёжности.
Билет №14
1. Адаптация управления набором высоты и скорости к реальным условиям полета, к характеристикам ЛА и его двигательной установки.
2. Способы управления угловым движением, движением центра масс ЛА.
На ракету в полёте действуют аэродинамические, реактивные и гравитационные силы. Из этих 3 групп сил для управления ракетой посредством органов управления можно использовать только аэродинамические и газодинамические (реактивные) силы.
Рассмотрим принцип использования аэродинамических сил для управления полётом. Аэродинамические органы управления делятся на рулевые отклоняющие поверхности (рули), поворотные крылья и прерыватели воздушного потока (интерцепторы).
Принцип действия рулей и поворотных крыльев.
Воздушный поток, обтекающий рули, приводит к появлению добавочных осевой и нормальной сил за счёт отклонения рулей от нейтрального положения.
Рассмотрим действие рулей высоты, которые управляют углом тангажа:
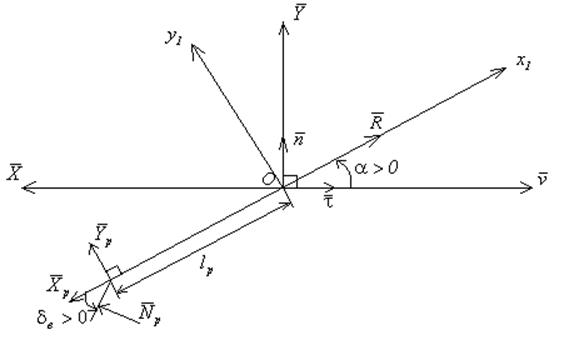
x1 - ось ЛА, точка О – ц.м., ![]() - вектор скорости ЛА
- вектор скорости ЛА
![]() , если подъёмная сила направлена вверх
, если подъёмная сила направлена вверх
Y- подъёмная сила, R- тяга
Х – сила лобового сопротивления
![]() - орт нормали к траектории ц.м.
- орт нормали к траектории ц.м.
![]() - орт касательной к траектории ц.м.
- орт касательной к траектории ц.м.
![]() - осевая и нормальная силы, действующие на
руль
- осевая и нормальная силы, действующие на
руль
![]() ,
, ![]() ,
,
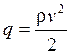
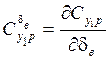
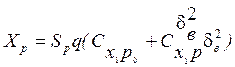
![]() ,
, ![]() -
аэродинамические коэффициенты
-
аэродинамические коэффициенты
![]()
![]()
Cxp, Cyp - коэффициенты силы лобового сопротивления и подъёмной силы руля
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.