Существенно улучшается согласование предшествующего участка траектории с экспоненциальной программой изменения высоты, если не фиксировать заранее значения Tэ и Нн = Нэ, а вычислять их в ходе полета, исходя из следующих условий в момент t = tн:
;
;
;
.
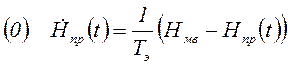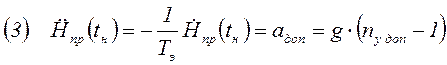Заранее
задается только допустимый уровень нормального ускорения 
.
Из соотношений (2) и (3):
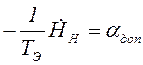или
(*)
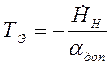Из (0), (1) и (2):
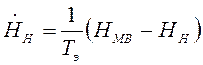
Подставив сюда выражение для ТЭ по (*), получаем
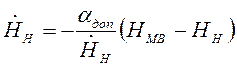, что
дает условие для фиксации момента tH:
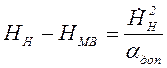, то
есть переход на «экспоненциальное уравнение» осуществляется в момент, когда
(**)
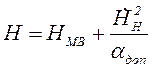По
из (*) определяется ТЭ;
все параметры экспоненциальной программы оказываются определенными и наилучшим
образом согласованными с условиями задачи.
; 
;
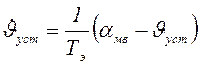при 
Экспоненциальная программа не оптимальна – затягивается выход на НМВ. Этот недостаток ослабляют, например, делая ТЭ убывающей функцией времени.
Использование экспоненциальной программы естественно, если в момент ее включения процесс Н(t) уже изменяется в направлении НК. Желание расширить область возможных сочетаний начальных условий привело к предложению использовать программу, формируемую как решение дифференциального уравнения
с начальными условиями:
x0 = HH и
(в дальнейшем для определенности полагаем Т1>Т2).
Однако,
решение этого уравнения при 
имеет вид:
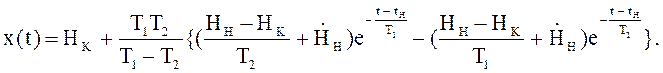
Разность двух экспонент с различными постоянными времени может приводить к немонотонному характеру процесса Н(t). Условие монотонности:
соответствует "подныриванию" ЛА под чисто экспоненциальную программу с соответствующей постоянной времени в начале движения по ней.
Чем больший выигрыш по снижению второй производной в момент начала движения по программе "с двумя экспонентами" мы имеем, тем сильнее может проявиться немонотонность изменения программы.
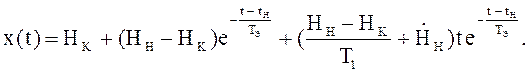
В этом случае для монотонности процесса Н(t) требуется строгое равенство
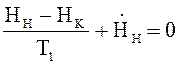, соответствующее
условию включения чисто экспоненциальной программы. Время выхода на малую
высоту при этом удваивается по сравнению с временем движения по программе с
одной постоянной времени ТЭ.
Выход из пикирования производится на высоту НМВ, априорно выбранную с запасом (по оценкам ошибок измерения высоты, неровности подстилающей поверхности, возможной амплитуды колебаний высоты полета). В процессе выхода на малую высоту производится уточнение фактического минимального превышения высоты полета над подстилающей поверхностью и подстройка установки НМВ. Таким образом, осуществляется адаптация к фактическим условиям полета.
Влияние параметров алгоритма управления на критические параметры полета достаточно сложно (уровни установок J1 и ограничения на скорость их изменения одновременно влияют практически на всю совокупность ограничиваемых переменных). Требуется еще и учет влияния ветровых порывов, вариаций атмосферных условий, характеристик ЛА, его двигательной установки и СУ. Поэтому синтез ведется в несколько приближений: после выбора структуры закона управления и первой аналитической оценки его параметров на основе только что изложенных соображений проводится серия расчетов – моделирование с использованием полной пространственной системы уравнений динамики управляемого полета с целью уточнения номинальных настроек и их влияния на ограничиваемые параметры полета. На заключительном этапе синтеза решается задача линейного программирования на минимизацию дистанции снижения с учетом ограничений. Влияние вариаций параметров на критерий оптимальности решения и на ограничиваемые величины считается аддитивным:
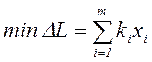
при
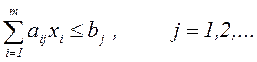(по всем режимам полета и всем контролируемым
ограничениям на поведение ЛА);
- поправки к выбранным настройкам,
и 
-
коэффициенты влияния,
- ограничения.
Результаты синтеза проверяются статистическим моделированием, полунатурным моделированием с реальными рулевыми приводами и прибором инерциальной навигации и автопилотирования. Заключительным этапом проверок являются летные испытания ЛА.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.