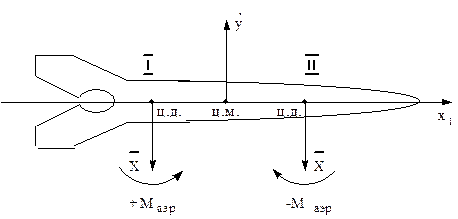
рис. 17
![]() – аэродинамический коэффициент,
учитывающий влияние угловой скорости на угловое движение (коэффициент
демпфирования). У баллистических ракет этот коэффициент мал, и приближённо его
можно не учитывать.
– аэродинамический коэффициент,
учитывающий влияние угловой скорости на угловое движение (коэффициент
демпфирования). У баллистических ракет этот коэффициент мал, и приближённо его
можно не учитывать.
рис. 18
![]() – коэффициент флюгерной устойчивости. Этот
коэффициент оказывает существенное влияние на динамику системы и пренебрегать
им нельзя. Для баллистических ракет и ракетоносителей можно считать, что
– коэффициент флюгерной устойчивости. Этот
коэффициент оказывает существенное влияние на динамику системы и пренебрегать
им нельзя. Для баллистических ракет и ракетоносителей можно считать, что ![]() . Ещё можно сказать, что это коэффициент
влияния угла тангажа на угловое движение по тангажу.
. Ещё можно сказать, что это коэффициент
влияния угла тангажа на угловое движение по тангажу.
рис. 19
![]() – коэффициент, учитывающий влияние
отклонения рулей на угловое движение, или эффективность рулевых органов.
Оказывает сильное влияние, так как управление должно пересиливать возмущение.
(см. рис. 19)
– коэффициент, учитывающий влияние
отклонения рулей на угловое движение, или эффективность рулевых органов.
Оказывает сильное влияние, так как управление должно пересиливать возмущение.
(см. рис. 19)
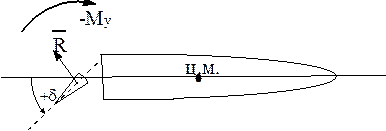
рис. 20
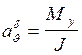
![]() – учитывает влияние скорости движения
центра масс на движение центра масс. Демпфирование всегда препятствует
движению, поэтому в уравнении перед этим коэффициентом стоит знак «минус».
Коэффициент мал и оказывает малое влияние на динамику системы, и в приближённых
расчётах им пренебрегают.
– учитывает влияние скорости движения
центра масс на движение центра масс. Демпфирование всегда препятствует
движению, поэтому в уравнении перед этим коэффициентом стоит знак «минус».
Коэффициент мал и оказывает малое влияние на динамику системы, и в приближённых
расчётах им пренебрегают.
![]() – коэффициент влияния углового положения
на движение центра масс. Это не аэродинамический коэффициент. Влияние
происходит в связи с тем, что двигатель жёстко закреплён на корпусе. Поэтому
при появлении J появляется составляющая силы тяги на ось уп.
– коэффициент влияния углового положения
на движение центра масс. Это не аэродинамический коэффициент. Влияние
происходит в связи с тем, что двигатель жёстко закреплён на корпусе. Поэтому
при появлении J появляется составляющая силы тяги на ось уп.
рис. 21
рис. 22
Если двигатель жёстко крепится на корпусе, то управление движением центра масс осуществляется за счёт изменения углового положения ЛА.
![]() – учитывает влияние отклонения рулей на
движение центра масс. Он относительно мал, и им можно пренебречь. Его роль по
сравнению с
– учитывает влияние отклонения рулей на
движение центра масс. Он относительно мал, и им можно пренебречь. Его роль по
сравнению с ![]() несущественна.
несущественна.
рис. 23
Все прочие уравнения можно найти в книге Б.М. Макарьева и Б.Р. Андриевского «Системы стабилизации летательных аппаратов. Принципы построения и структура систем стабилизации».
Преобразуем уравнения (1) и (2), заменив в них символ дифференцирования на р.
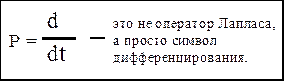
Преобразование Лапласа уводит из временной области в комплексную. При символической записи мы остаёмся во временной области, не смотря на внешнее сходство. Итак.

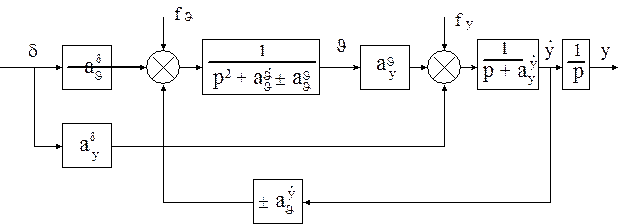
рис. 24
Теперь представим эти уравнения в виде структурной схемы.
При выборе системы управления первая операция состоит в определении устойчивости собственного движения ЛА (неуправляемого).
Пусть компоновка ЛА
статически устойчива, тогда ![]() берётся с
плюсом. Если же компоновка статически неустойчива, тогда
берётся с
плюсом. Если же компоновка статически неустойчива, тогда ![]() с минусом, и звено будет неустойчивым, но
зато и
с минусом, и звено будет неустойчивым, но
зато и ![]() с минусом, и обратная связь
станет отрицательной, то есть будет способствовать устойчивости. Но
неустойчивость звена сказывается сильнее, чем отрицательная обратная связь.
Таким образом, в любом случае движение ЛА неустойчиво, и требуется система
управления.
с минусом, и обратная связь
станет отрицательной, то есть будет способствовать устойчивости. Но
неустойчивость звена сказывается сильнее, чем отрицательная обратная связь.
Таким образом, в любом случае движение ЛА неустойчиво, и требуется система
управления.
Чем же можно пренебречь при приближённых исследованиях. Допустимые упрощения показаны на рис. 25.
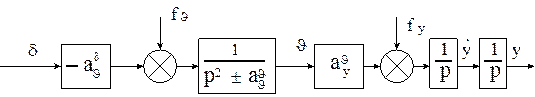
рис. 25
То есть угловое движение можно рассматривать без учёта движения центра масс, но наоборот нельзя.
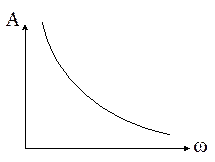
Параметры движения центра
масс ![]() с угловыми параметрами J связаны интегральными зависимостями. АЧХ интегрирующих звеньев
падающие. Это указывает на то, что движение центра масс более низкочастотное,
чем угловое движение. Сейчас частоты управляемого углового движения порядка
0,01Гц, а частоты управляемого движения центра масс на порядок меньше.
с угловыми параметрами J связаны интегральными зависимостями. АЧХ интегрирующих звеньев
падающие. Это указывает на то, что движение центра масс более низкочастотное,
чем угловое движение. Сейчас частоты управляемого углового движения порядка
0,01Гц, а частоты управляемого движения центра масс на порядок меньше.
Билет №15
1. Построение управления на участке снижения на малую высоту.
Основу управления на участке снижения составляет управление тангажом.

Элементы адаптации к фактическим условиям полета именно в этом наборе событий.
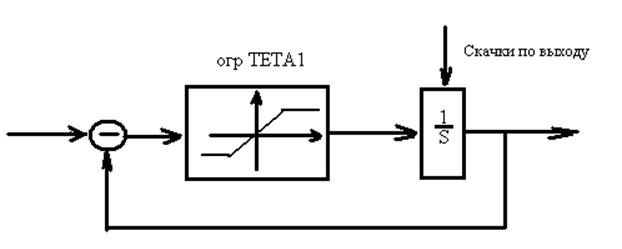
Следует добавить управление по высоте

Предусматривается переходный участок (перегрузка и балансировка плавно изменяется)
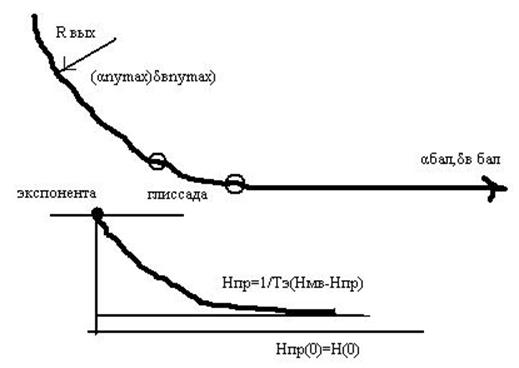
Через 4 секунды после прохождения высоты 1200м.
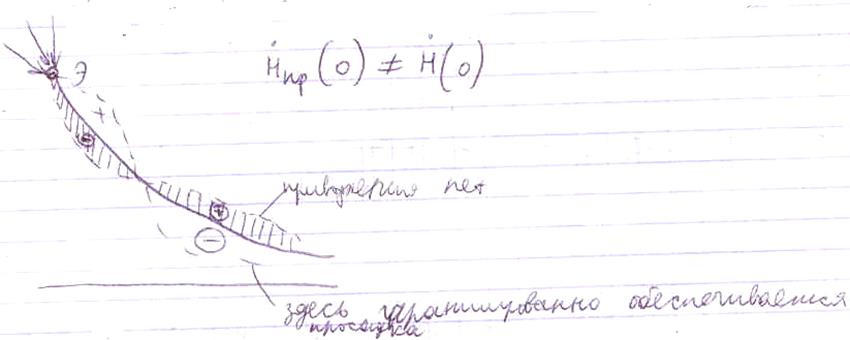
Управление гарантируется астатически.
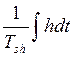 ,
,
Тогда составляется уравнение
![]() (малая высота)
(малая высота)
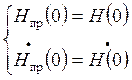
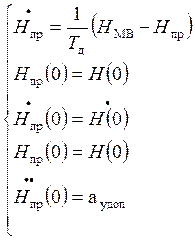 Экспонента хороша тем, что по всем ее производным
максимум в нуле.
Экспонента хороша тем, что по всем ее производным
максимум в нуле.
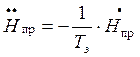 ,
,
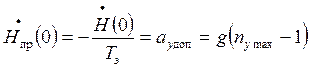 ,
,
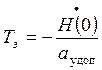 , подставим в 1-е уравнение
, подставим в 1-е уравнение ![]() поменяем просто на
поменяем просто на ![]() .
.
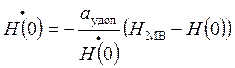 - это условие, связывающие высоту и
скорость ее изменения в момент когда перегрузка максимальна (момент подключения
глиссады).
- это условие, связывающие высоту и
скорость ее изменения в момент когда перегрузка максимальна (момент подключения
глиссады).
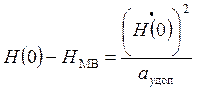 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.