Транспортировка пучка. Оптика пучка в отсутствие коллективных эффектов. Теорема Буша и уравнение параксиального луча, страница 9

Это уравнение может быть дважды проинтегрировано для получения решения. Харрисон [14] рассмотрел частный случай уравнения (48), когда r_о - а меньше, чем a, которое равно r_о при r₀', равном нулю. Решением является гипербола вида

                                                                                                                                       (50)

с асимптотическим углом расходимости . Отсюда следует, что параксиальная форма справедлива, если только К много меньше единицы.

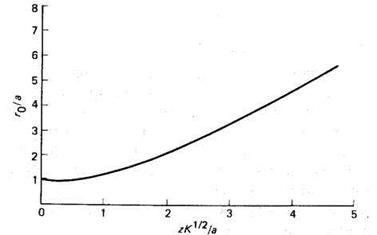
Рис. 4.9. Расширение пучка от минимального радиуса а с первеансом К под действием нескомпенсированного объемного заряда пучка, r₀/a — безразмерный радиус огибающей; z K^1/2 a— безразмерное расстояние вдоль оси.

Точное решение уравнения (48) есть

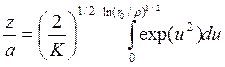 при K > 0

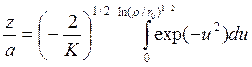 при K < 0

Интеграл может быть рассчитан численными методами, и зависимость  от  показана на рис. 4.9. При положительных К кривая очень близка к гиперболе, что можно видеть на рисунке. Когда К отрицательно, пучок быстро сходится и распространяется на очень незначительное расстояние вдоль оси пучка, прежде чем траектории пересекут ось в месте перетяжки пучка. Последняя ситуация нестандартна и имеет место, если только h очень близко к единице или превышает ее.

Свидетельство относительной важности обобщенного первеанса может быть получено при выводе предельного значения плотности тока , когда объемный заряд пучка вызвал бы 10%-ное (например) увеличение диаметра пучка. Из уравнения (50) следует . Поэтому

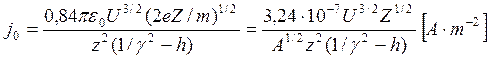                                        (52)

Здесь А — масса иона, выраженная в массах протона (U выражается в вольтах, a z — в метрах). Уравнение (52) показывает, что ток j0, который может быть транспортирован на значительное расстояние (т. е. на расстояние, составляющее много диаметров пучка) очень мал, когда h мало по сравнению с единицей. Если h равно нулю, только релятивистские пучки могут быть транспортированы на значительное расстояние при высоких плотностях тока. Однако существует несколько методов улучшения транспортировки пучка, которые обсуждаются в следующих разделах.

4.2.2. Собственные поля и уравнение параксиального луча

Если собственные поля, вызывающие поперечное движение ионов, создают скорости ионов, которые малы по сравнению с осевой скоростью, эти поля могут быть учтены в уравнении параксиального луча, приведенного в разд. 4.1.1. Используя уравнение (48) для вывода дополнительного радиального ускорения, при сложении уравнений (48) и (6), когда г = Го, получим

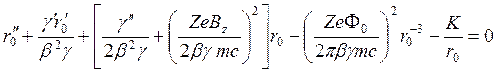                                      -(53)

Это уравнение показывает, что пучок может распространяться не расплываясь, когда Ф_о равно нулю, если обобщенный первеанс К связан с аксиальной составляющей магнитной индукции B_z соотношением

                                                                                                                       (54)

Это условие определяет поток Бриллюэна и детально обсуждается в следующем разделе.

4.2.3. Распространение пучка в аксиальном магнитном поле

В разд. 4.1.1 мы уже рассмотрели движение ионов в аксиальном поле (теорема Буша) и уравнение параксиального луча. В простом случае однородного нерелятивистского пучка с объемным зарядом, для которого h (степень нейтрализации) равна нулю, можно написать соотношение

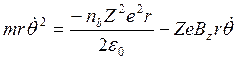
в предположении, что пучок находится в состоянии жесткого ротатора, так что — постоянная величина. Написанное соотношение можно привести к виду

где  — ларморовская частота () и  — плазменная ионная частота пучка  . Это уравнение имеет решения

                                                                                                            (55)

При условии, что   , существуют два действительных решения для, одно из которых больше, а другое меньше ларморовской частоты. Условие

                                                                                                                                      (56)