Транспортировка пучка. Оптика пучка в отсутствие коллективных эффектов. Теорема Буша и уравнение параксиального луча, страница 14

Следовательно, имеющиеся теоретические модели описывают только последний случай, который, конечно, очень похож на нейтрализацию пучка положительных ионов, за исключением другого знака пространственного заряда пучка. Новая модель Райта [27] объясняет переход между этими двумя состояниями нейтрализации, хотя она является чисто численной и не дает законы масштабирования. В работах [28, 20] предложены одномерные модели, основанные на дрейфе ио-нов плазмы и описывающие плазму пучка с положительной потенци-альной ямой. Однако ни одна из этих моделей не содержит основной процесс подвода энергии, формирующий распределение электронов, образующихся при обдирке отрицательных ионов в столкновениях с молекулами остаточного газа. В этом процессе получаются электро-ны, имеющие ту же скорость, что и ионы пучка. Значение такого про-цесса возрастает по мере того, как увеличивается энергия пучка. Остальные процессы почти идентичны процессам, описанным для пучка положительных ионов. Существует баланс между производством и потерей электронов, а также положительных ионов, и вновь предполагается нейтральность плазмы. В следующем разделе описа-нa простая одномерная модель для плазмы пучка отрицательных ио-нов, основанная на рассмотрении всех указанных процессов.

Простая модель нейтрализации пучка отрицательных ионов.

В пучке отрицательных ионов существуют два основных процесса взаимодействия между ионами пучка и молекулами газа:

1) ионизация

2) отщепление электронов

,или

где A ^- — ион пучка и Х° — молекула газа. Подчеркивание обозначает быструю частицу. В отличие от пучка положительных ионов эти процессы создают больше электронов, чем положительных ионов.

Уравнение непрерывности для медленных положительных ионов приводит к выражению, которое в основном совпадает с уравнением (67), за исключением того, что пространственный потенциал, вероятно, будет так мал при низких давлениях газа, что влияние малой, но конечной температуры медленных ионов должно быть учтено. В пределе, когда потенциальной ямы пучка не существует, т. е. φ₀ = 0, плотность медленных ионов определяется формулой

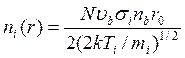                                                                                                                    (79)

Следовательно, мы можем эффективно объединить уравнения (79) и (67) путем сложения эффективных энергий ионов в знаменателе в случае, когда имеются как конечная температура ионов, так и потенциал пучка.

Результирующее выражение для плотности медленных ионов, следовательно, имеет вид

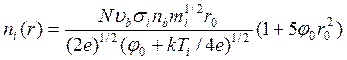                                                                            (80)

где φ_о и φ₁ — величины, определенные в уравнении (66), и kT- ионная температура.

В случае положительно заряженных ионов величина T_i была много меньше, чем φ_о и потому ею можно было пренебречь. Электроны плазмы подчиняются распределению Больцамана, так что

                                                                         (81)

тогда как баланс между создаваемыми и уходящими электронами в пределах поперечного сечения пучка дает соотношение

                                                                            (82)

где φ_w — потенциал на границе пучка и по предположению  равно тепловой скорости на границе пучка. Таким образом, получаем выражение, идентичное тому, которое было выведено для пучка положительных ионов.

Однако уравнение баланса энергии существенно отличается от уравнения для пучка положительных ионов из-за наличия энергичных электронов, отщепляющихся от отрицательных ионов. Начальная скорость этих электронов направлена вдоль оси пучка; впоследствии скорость электронов приобретает равномерное распределение по степеням свободы в результате электрон-электронных и электрон-молекулярных столкновений. Если предположить, что этот процесс доминирует над всеми остальными при высоких энергиях пучка, то средняя энергия ε_е, приходящаяся на созданный электрон, равна

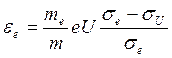                                                                                                                       (83)