Транспортировка пучка. Оптика пучка в отсутствие коллективных эффектов. Теорема Буша и уравнение параксиального луча, страница 7

Зависимость от массы и скорости также позволяет использовать эти магниты для приборов селективного отбора по массе или импульсу.

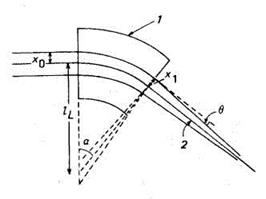
Рис. 4.7. Фокусирующее действие секторного отклоняющего магнита. 1 — поверхность полюсного наконечника секторного магнита; 2 — равновесная траектория.

Такие магниты могут действовать как толстые линзы, когда полный угол отклонения существенно меньше 180°. Метод, с помощью которого достигается фокусировка, иллюстрируется рис. 4.7; фокусирующий эффект достигается уменьшением длины внутренней траектории при прохождении через магнит. Для простого секторного магнита, показанного на рис. 4.6, где границы полюсов перпендикулярны оси пучка, уменьшение расстояния между осью и параллельной траекторией при начальном расстоянии x₀ определяется формулой x₁ = x_о cos α, где α — угол при вершине сектора магнита. Используя геометрические соотношения (рис. 4.7), можно показать, что в  и, следовательно,

                                                                                                                                (33)

Часто бывает удобно выразить эти соотношения в матричной записи, которая для секторного магнита имеет вид

Mm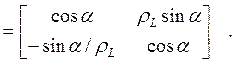                                                                                                 (34)

Как и для всех матриц, приведенных выше, детерминант данной матрицы равен единице.

Фокусирование пучка также происходит, когда ионный пучок входит в зазор под углом к границам полюсов магнита, под влиянием той составляющей основного поля у полюса магнита, которая ортогональна направлению пучка (рис. 4.8). Когда пучок входит в магнит и выходит из него нормально к границам полюсов, Вх = 0. Следовательно, никакой фокусировки затем не наблюдается.

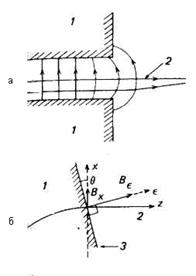
Рис. 4.7. Фокусирующее действие секторного отклоняющего магнита. 1 — поверхность полюсного наконечника секторного магнита; 2 — равновесная траектория.

Фокусное расстояние, определяемое таким эффектом, может быть получено посредством вычисления изменения поперечного импульса , приобретенного частицей при движении в направлении, перпендикулярном к торцу, который наклонен под углом θ к оси пучка. Простой метод анализа предложенный Хамфризом [12], показывает, что  , но  , где  — поле, действующее у полюса магнита, и  . Следовательно,

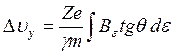                                                                                                                       (35)

Так как дивергенция В равна нулю, можно показать, что  , где Bо — магнитная индукция основного поля в промежутке. Следовательно, так как поперечная составляющая скорости пропорциональна у, понятие «фокусное расстояние» верно, и можно показать, что

                                                                                                                              (36)

Если θ больше нуля, то магнит обеспечивает вертикальную фокусировку, но уменьшает горизонтальную фокусировку. В такой ситуации секторный магнит может обеспечить фокусировку в обеих плоскостях, и это свойство используется при конструировании безградиентного синхротрона [13].

4.1.4. Каналы транспортировки пучка

Матричный метод, выражающий свойства линзы или пролетного промежутка, позволяет непосредственно определить действие последовательности таких элементов. Если траектория ионов пересекает последовательно элементы системы, свойства каждого из которых могут быть выражены последовательностью матриц А, В, С, ... , то конечная траектория  может быть записана в виде

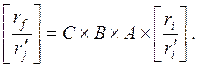                                                                                                                 (37)

Надо отметить, что порядок следования матриц А, В, С должен в точности соответствовать последовательности расположения элементов на пути частицы, поскольку произведение матриц не коммутативно. В качестве примера рассмотрим пролетный промежуток длиной l/2, линзу с фокусным расстоянием  и еще один пролетный промежуток. Комбинированная матрица С равна произведению матриц: